- الأنظمة المعرفية الإبداعية، الحوسبة التي تركز على الإنسان، معهد علوم الكمبيوتر، جامعة برلين الحرة، برلين، ألمانيا
إعادة التمثيل هي قدرة حاسمة على (1) فهم الحلول الإبداعية للمشكلات البشرية، و (2) نمذجة الأنظمة المعرفية الحسابية القادرة على دعم أو أداء مهام حل المشكلات الإبداعية بمفردها. تقترح هذه الورقة نهجًا معرفيًا موحدًا متعدد المستويات لدراسة إعادة التمثيل: دراسة الأشكال الممكنة لإعادة التمثيل القائمة على الحواس والمفاهيم والقالب القائم على المشكلة بطريقة متكاملة. الأوصاف والتفسيرات لكل مستوى تمهد الطريق لمزيد من النمذجة الحسابية. يتم نشر دراسة من أجل استكشاف العلاقة بين المهام المختلفة المقترحة لتعكس إعادة التمثيل. تم اكتشاف وجود علاقة ذات دلالة إحصائية بين المهام التي تم التحقيق فيها. يتم تكرار دراستين سابقتين من الأدب.
1 المقدمة
تخيل أنك تواجه مشكلة، وحاول حلها دون جدوى لمدة نصف ساعة. وبعد فترة من الوقت، تأخذ استراحة منه وتركز على شيء آخر. وفي منتصف هذا النشاط الآخر، تتبادر إلى ذهنك طريقة مختلفة تمامًا لرؤية مشكلتك السابقة. يبدو الأمر كما لو أن عناصر المشكلة قد تغيرت، وأعيد تنظيمها في هذه الأثناء؛ أنك الآن تفهم ما هو المهم حقًا، وكيف كان ينبغي عليك معالجة المشكلة في المقام الأول. ستختبر لحظة من الوضوح والوعد: هذه الطريقة الجديدة لرؤية المشكلة قد تسمح لك بإيجاد الحل، أو على الأقل تحقيق المزيد من التقدم. من المحتمل جدًا أنك، في الحالة المذكورة أعلاه، قد واجهت حالة إعادة تمثيل.
إعادة التمثيل هي قدرة معرفية بشرية تتم مواجهتها في عمليات الإبداع وحل المشكلات بشكل إبداعي. من منظور حسابي، فإن الفهم والنمذجة الأفضل لإعادة التمثيل سيمكننا ليس فقط من دراسة المهارة المعرفية إلى مستوى أعمق، ولكن أيضًا من تنفيذ الجيل القادم من اكتشاف المعرفة وأنظمة حل المشكلات الإبداعية للإلهام المعرفي. سيكون للنظام الحسابي الذي يتمتع بإعادة التمثيل نفس القدرة على عرض المشكلات ومجموعات البيانات بطرق مختلفة، وتوليد مسارات حلول إبداعية وثاقبة جديدة واكتشاف معرفة جديدة. مع كون إعادة التمثيل عملية معرفية من المحتمل أن تصبح التحدي التالي في الأنظمة القائمة على المعرفة، فإن الأسئلة البحثية الرئيسية التي يتم تناولها هنا هي: (أ) كيف يمكننا أن نفهم بشكل أفضل، توصيف ودراسة قدرات إعادة تمثيل العقل البشري بشكل تجريبي، (2) كيف يمكننا أن نبدأ في تصورها ونمذجتها عبر تقنيات النمذجة الحسابية؟ و (3) هل هناك وعد بأن المهام الحالية من الأدبيات التجريبية يمكن استخدامها لدراسة إعادة التمثيل بطريقة متماسكة؟
تمت دراسة القدرات المعرفية المختلفة المتعلقة بالإبداع في الأدبيات، مع تنفيذ أنظمة حسابية قادرة على تحقيق إنجازات مماثلة في بعض الأحيان. ومن أمثلة هذه القدرات: الارتباط عن بعد ( Mednick and Mednick, 1971 ; Olteţeanu and Falomir, 2015 ; Olteţeanu et al., 2017 , 2018 ) والقياس ( Gentner, 1983 ; Falkenhainer et al., 1989 ; Holyoak and Thagard, 1996 ) ، استعارة ( لاكوف وجونسون، 1980 ، 1999 ؛ فيل وهاو، 2008 )، مزج المفاهيم ( فوكونير وتيرنر، 1998 ؛ إيبي وآخرون، 2015) .) وما إلى ذلك. كونها جزءًا من عائلة المهارات المعرفية الإبداعية، فإن القدرة على إعادة التمثيل قد (1) تكون مرتبطة أو مشابهة لبعض مهارات الإبداع (على سبيل المثال، القياس والاستعارة)، أو (2) تستخدم مهارات أخرى يعتمد عليها الإبداع تعتمد العملية على (على سبيل المثال، الارتباط). ومع ذلك، قبل تقديم أي ادعاءات فيما يتعلق بالعلاقات مع المهارات أو العمليات المعرفية الإبداعية الأخرى، من الضروري اتباع نهج منهجي أقوى للفهم العام وتوصيف ودراسة إعادة التمثيل.
توجد بنيات معرفية مختلفة بأنواع مختلفة من الالتزامات النظرية والتمثيلية، تُستخدم لنمذجة مجموعات مختلفة من المهام والعمليات: ACT-R ( Lovett, 1998 )، SOAR ( Laird et al., 1987 )، CLARION ( Sun, 2007) )، EPIC ( Kieras and Meyer، 1997 )، Leabra ( O’Reilly، 1996 )، SAL ( Jilk et al.، 2008 )، وما إلى ذلك. ومع ذلك، لا تتعامل مثل هذه الهندسة المعمارية مع العمليات الإبداعية بطريقة موحدة. وقد تم اقتراح مناهج موحدة لبعض العمليات ( Olteţeanu, 2014 ; Olteţeanu, 2016 )، لكنها لا تتضمن بعد إعادة التمثيل.
لبدء التوحيد في هذا الاتجاه، يجب دراسة إعادة التمثيل كعملية في مجموعة متنوعة من البيئات المختلفة، بحيث يمكن للإطار المعرفي الذي يستوعب جانبًا واحدًا من العملية أن يتعامل أيضًا مع مظاهرها الأخرى. في الروح الموحدة للبنى المعرفية التي طرحها نيويل (1994)تقترح هذه الورقة أن الأطر المعرفية التي تهدف إلى دراسة وتنفيذ إعادة التمثيل ستحتاج إلى القيام بذلك بشكل منهجي على مستويات مختلفة من المهارات المعرفية. وهذا يتطلب تحديد مستويات مختلفة لديها فرص للتوحيد من خلال نفس العملية، والقيام بذلك من خلال المصطلحات التي تجعل العملية قابلة للتنفيذ الحسابي. هنا، يُقترح نهج يتم من خلاله استكشاف مستويات متعددة محتملة لإعادة التمثيل، وتتم مناقشة هذه المستويات في مصطلحات النمذجة الحسابية. الهدف الرئيسي هو وضع أساس نحو الدراسة التجريبية والحاسوبية السليمة لإعادة التمثيل في البنى المعرفية. ترتبط هذه المستويات بمهام إبداعية محددة موجودة، لتقديم فرصة جيدة للتزوير التجريبي لفرضية دراسة إعادة التمثيل الموحدة هذه، ومعيارًا قويًا لمقارنة النماذج الحسابية المستقبلية بها. يتم نشر دراسة استكشافية لتأكيد أو دحض العلاقات الأولية بين هذه المهام.
يتم تنظيم بقية هذه الورقة على النحو التالي: تم وصف المستويات الثلاثة لإعادة التمثيل لأول مرة في القسم 2. ويتم استكشاف المستوى الأول – من إعادة تمثيل الميزة إلى الكائن – في المصطلحات الحسابية والنمذجة المحتملة في القسم 3. أما المستوى الثاني المستوى – إعادة تمثيل الكائنات والخصائص – موصوف في القسم 4. تم استكشاف المستوى الثالث – إعادة تمثيل الكائنات وقالب المشكلة – في القسم 5. تم الإبلاغ عن الدراسة المنشورة لاستكشاف العلاقة بين هذه المهام في القسم 6 تمت مناقشة نظرة عامة على أوجه التشابه والاختلاف والتفاعل المحتملة بين المستويات المختلفة في القسم 8، بالإضافة إلى نتائج الدراسة.
2. ثلاثة مستويات من إعادة التمثيل موصوفة من خلال مهام إبداعية مختلفة
فيما يلي، سيتم وصف أربع مهام إبداعية مختلفة لحل المشكلات بإيجاز، بالإضافة إلى علاقاتها المحتملة بالقدرة على إعادة التمثيل. المهام هي:
1) مهمة الأرقام الغامضة؛
2) اختبارات النمط ومعاني الخطوط ( والاش وكوجان، 1965 )؛
3) اختبار الاستخدامات البديلة ( جيلفورد وآخرون، 1978 ) و
4) مشاكل البصيرة ( ماير، 1931 ؛ دنكر، 1945 ؛ داو وماير، 2004 ).
واستناداً إلى هذه المهام الأربع، سيتم مناقشة ثلاثة مستويات محتملة لإعادة التمثيل.
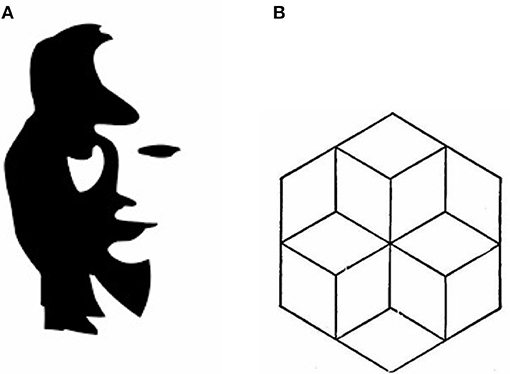
تخيل أنك تنظر إلى شخصية غامضة ، مثل تلك الموضحة في الشكل 1 ، ولا يمكنك رؤية أرنب إلا في البداية. قد يُقال لك أنه يمكن أيضًا رؤية صورة مختلفة (بطة)، فتحاول رؤيتها طوعًا، أو قد تواجه لحظة مفاجئة عفوية “تنبثق” فيها الصورة الثانية فجأة. يمكنك الآن على الأرجح التبديل بين رؤية هذه الصور المختلفة حسب الرغبة. في الواقع، قد يُطلب من المشاركين الذين عُرضت عليهم هذه المهمة الضغط على زر في كل مرة يكونون قادرين فيها على تبديل تمثيلهم للحافز ( Doherty and Mair, 2012 ) – ويسمى هذا القياس التقييمي بتردد الانعكاس. كيف ترتبط الأرقام الغامضة بإعادة التمثيل؟ يقترح منهجنا أن الصور الغامضة يمكن أن تمثل مستوى من القدرة يتضمن مستوى القدرة على إعادة تمثيل الميزات المرئية في الصور ككائنات أو كيانات مختلفة محتملة.
الشكل 1 . وهم أرنب البط.
إن اختبار معاني النمط الذي أجراه والاش وكوجان (1965) يعطي المشاركين محفزات نمطية مجردة مثل تلك الموضحة في الشكل 2أ . تتمثل مهمة المشاركين في الوصف، شفهيًا أو كتابيًا، لكل الأشياء التي يعتقدون أن هذه الأنماط يمكن أن تكونها، أو كل الأشياء التي تذكرهم بها هذه الأنماط (لاحظ الإشارة إلى الذاكرة، والتي سنلتقطها مرة أخرى في هذا المقال) القسم 3.2). على سبيل المثال، يمكن رؤية النمط الموجود في الشكل 2أ على أنه مجموعة من المقاعد أمام طاولة، أو أشخاص ينتظرون في طابور بجوار مبنى، أو رؤوس زهور قادمة من أصيص زهور مستطيل، أو لعبة مهد نيوتن، وما إلى ذلك.
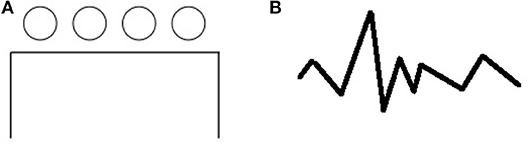الشكل 2 . اختبارات الإبداع من قبل والاش وكوجان (1965) . (أ) اختبار معاني النمط. (ب) اختبار معاني الخط.
يتم تقديم مهمة مماثلة من خلال اختبار معاني الخط ( والاش وكوجان، 1965 )، حيث يتم عرض خط مثل ذلك الموجود في الشكل 2ب ، ويجب على المشاركين التوصل إلى أشياء يمكن أن يكون عليها الخط – على سبيل المثال محيط الخط سلسلة جبلية، ومنشار غير مستوي، ومشط ذو أسنان مكسورة، وما إلى ذلك1 .
تشترك اختبارات معنى النمط ومعنى الخط في ما يلي: خلال كلتا المهمتين، يتم إعادة تمثيل الحافز المجرد (أو مجموعة من الميزات) بشكل متكرر من قبل المشاركين من خلال تمثيلات معروفة مختلفة.
يعد عدد التفسيرات البديلة التي توصل إليها المشاركون جزءًا من تقييم النتائج في اختبارات النمط ومعنى الخط. لا يزال من الممكن وضع هذا النوع من التفسير وإعادة التمثيل على مستوى تفسير الميزات كأشياء. على عكس مهمة الأشكال الغامضة، فإن الأشياء التي يتم من خلالها إعادة التمثيل لا تقتصر على اثنين، ولا تكون موجودة في الشكل؛ يعتمدون على معرفة الحلال. ولهذا السبب، هناك أكثر من تفسيرين ممكنين أيضًا (يمكن تمثيل الأرقام الغامضة عمومًا بطريقتين، أو بحد أقصى ثلاث طرق).
اختبار الاستخدامات البديلة بواسطة جيلفورد وآخرون. (1978) يعطي المشاركين شيئًا ما، ويطلب منهم التوصل إلى أكبر عدد ممكن من الاستخدامات له. على سبيل المثال، يتم إعطاء الكائن “الطوب”، ويمكن للمشاركين التوصل إلى استخدامات مثل ما يلي: يمكن استخدام الطوب كثقالة للورق، أو كسلاح، أو كمصد للباب، أو حول النار، أو للكتابة على الرصيف، وما إلى ذلك.
ومن أجل ربط هذه المهمة بإعادة التمثيل، لا بد من النظر في عملية التوصل إلى استخدامات محتملة مختلفة. اقتراح لكيفية القيام بهذا النوع من الاستدلال الإبداعي (التوصل إلى استخدامات بديلة للأشياء) هو ما يلي: بعد إعطاء الكائن (على سبيل المثال، خيط تنظيف الأسنان)، خصائصه (الشكل، الوزن، المادة، الحجم) و يتم إعادة تمثيل مجموعاتها كأشياء أخرى محتملة (شكل والمادة المستخدمة في خيط تنظيف الأسنان تجعل من السهل إعادة تمثيل هذا الكائن كقطعة طويلة من الخيط، على سبيل المثال). بعد ذلك، يمكن تطبيق إمكانيات الأشياء التي تم إعادة تمثيلها فيها مرة أخرى على الكائنات الأولية (على سبيل المثال، يمكن استخدام خيط تنظيف الأسنان للخياطة). هذا الاستدلال بالذات هو في الواقع جزء من مجموعة الاستدلالات الإبداعية التي يتم إجراؤها بواسطة نظام ينفذ هذه العملية حسابيًا ( Olteţeanu and Falomir، 2016 ).
وبالتالي فإن هذا هو الحال بالنسبة لإعادة التمثيل إذا تم تفسير خصائص أو سمات كائن ما على أنها خصائص وسمات كائن آخر، من أجل التوصل إلى القدرة الجديدة. لذلك، قد يتضمن اختبار الاستخدامات البديلة مستوى القدرة على إعادة تمثيل الأشياء وخصائصها ككائنات مختلفة في بيئة المجال المنزلي، حتى تتمكن من التوصل إلى استخدامات إبداعية للأشياء المذكورة. هذا المستوى من إعادة التمثيل، إلى جانب العملية التي من خلالها ينتج OROC ( Olteţeanu and Falomir, 2016 )، وهو نموذج أولي لنظام حسابي قادر على أداء هذه المهمة، إجابات، بمزيد من التفاصيل الحسابية في القسم 4.
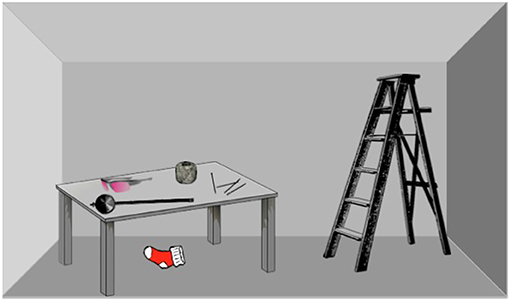
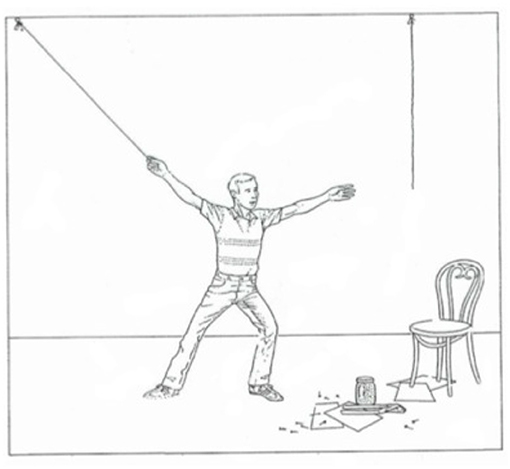
تمثل مشكلات البصيرة مهامًا أكثر تعقيدًا، حيث يتم تقديم مجموعة من الكائنات (الكائنات اليومية أو الكائنات المجردة أو في بعض الأحيان مجرد أنماط) في علاقات مختلفة إلى المحلل. على سبيل المثال، تم توضيح مشكلة الوزن ( Dunker, 1945 )، والتي أوضحناها في الشكل 3 ، على النحو التالي: عليك أن تساعد المراقب في إعداد الغرفة لإجراء التجربة. تحتاج إلى إرفاق البندول بالسقف. ماذا تفعل؟
الشكل 3 . مشكلة الوزن.
يبدأ المشاركون في التفكير في خطط عمل مختلفة (تتضمن مجموعات من الإجراءات، ومجموعة من الأشياء وإمكانات الأشياء) التي يمكن أن تساعدهم في حل المشكلة. وبعد فترة، يتضح أن إحدى المسائل الأساسية لحل المشكلة هي إمكانية تثبيت أحد المسامير الموجودة على الطاولة بالسقف، وذلك لتثبيت الخيط على السقف وربط البندول به. تتم تجربة طرق مختلفة لتحقيق ذلك. المسار الإنتاجي هو محاولة إنشاء مطرقة من الأشياء الموجودة – ومحاولات تحقيق ذلك تتضمن حلولاً بشرية يقترحون استخدام الجزء العلوي من الدرج كمطرقة، أو لف بكرة الخيط أو النظارات البلاستيكية المطوية في جورب من أجل صنعها. “أصعب”، أو الحل الصحيح الذي قدمه دنكر، هو استخدام البندول نفسه لدق المسمار قبل ربطه بقطعة من الخيط. يُظهر هذا إعادة التمثيل في العمل في مشاكل الاستبصار – إعادة تمثيل بعض الكائنات (البندول) ككائن آخر مطلوب (المطرقة) – بنكهة مشابهة لعمليات OROC عند حل AUT. ومع ذلك، يمكن أيضًا تمثيل الكائنات ومجموعات الإجراءات المتعددة بطرق متعددة، باستخدام طرق معروفة بالفعل لحل المشكلات (ما نسميه قوالب المشكلات) ومجموعاتها الفرعية. ويرد فحص أعمق ومثال لهذا المستوى في القسم 5.
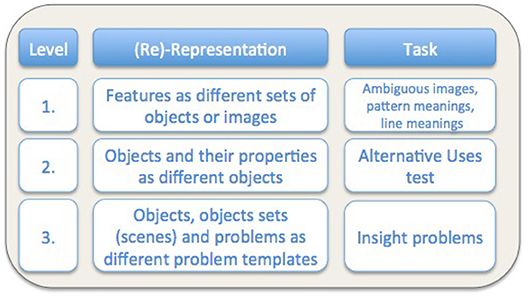
باختصار، المستويات الثلاثة التي يمكن من خلالها استكشاف إعادة التمثيل المقترحة هنا هي:
1. القدرة على إعادة تمثيل الميزات كمجموعات مختلفة من الكائنات أو الصور في حالة الأشكال الغامضة؛
2. القدرة على إعادة تمثيل الأشياء وخصائصها ككائنات مختلفة؛ سنناقش هذا بشكل عام في بيئة المجال المنزلي، مع التركيز على القدرة على استخدام الكائنات بشكل إبداعي عندما تكون الكائنات التقليدية التي سيتم استخدامها مفقودة2 و
3. القدرة على إعادة تمثيل الأشياء والمشاهد تحت قوالب مشكلة مختلفة، لتكون قادرة على معالجة حل مشاكل البصيرة البشرية في المستقبل حسابيا.
ويرد في الشكل 4 لمحة عامة عن مختلف مستويات إعادة التمثيل والمهام التجريبية التي يمكن من خلالها دراسة إعادة التمثيل على هذا المستوى . والمقصود بهذا بالطبع هو الرسم الأولي، وليس قائمة شاملة.
الشكل 4 . نظرة عامة على المستويات المقترحة لإعادة التمثيل.
تشير بعض الأدلة الأولية في اتجاه صحة مثل هذا النهج: لقد توقعت نظريات مختلفة العلاقة بين الشخصيات الغامضة والإبداع، وتم التعبير عن أقدمها في الحركة الجشطالتية (يمكن العثور على ملخص لطيف للآراء الجشطالية العامة حول إعادة الهيكلة في أولسون (1983 ، 1984) ). في الآونة الأخيرة، تم الحصول على التحقيقات التجريبية الأولى لإظهار النتائج في تأكيد هذا الاتجاه الفكري من قبل وايزمان وآخرون. (2011) ودوهرتي وماير (2012) . في وايزمان وآخرون. (2011) ، تمت ملاحظة وجود علاقة بين سهولة عكس الأرقام الغامضة والإبداع كما تم قياسه باستخدام مهمة الاستخدامات البديلة لجيلفورد (Spearman’s rho= 0.28، ع = 0.007). أظهر دوهرتي وماير (2012) وجود علاقة بين الأشكال الغامضة والإبداع كما تم قياسه باستخدام مهمة معاني النمط (Spearman’s rho = 0.42، p <0.01).
2.1. إعداد النهج
فيما يلي، سيتم تحليل كل مستوى من مستويات إعادة التمثيل من الناحية الحسابية، باستخدام سياق المهام التي تم تقديم نظرة عامة عليها في القسم 2. وبالتالي سيتم تحديد المستويات من حيث المدخلات والمعرفة الموجودة مسبقًا في النظام المعرفي والمخرجات وعمليات إعادة التمثيل.
هذه موصوفة أدناه:
1. المدخلات – تحدد المدخلات الحسية أو المفاهيمية الأولية للمهمة (من الناحية الموضوعية)، سواء كانت ميزات أو أشياء أو خصائصها أو مجموعات كائنات أو مشاهد أو مشاكل أو أوصاف لها؛
2. المعرفة الموجودة مسبقًا – تقدر نوع المعرفة التي يجب افتراض وجودها في النظام، حتى تكون عمليات إعادة التمثيل وأنواع مختلفة من المخرجات ممكنة؛
3. المخرجات – تمثل أنواع الصور والأشياء والاستخدامات ومجموعات الكائنات وخطط العمل (أو تمثيلاتها) التي هي نتائج تمثيل المشكلة وعملية إعادة التمثيل؛
4. إعادة التمثيل – العملية التي نحاول أن نلاحظها على هذه المستويات المختلفة، تأخذ في الاعتبار المعرفة والمدخلات الموجودة، لإنتاج أشكال مختلفة من المخرجات.
تستكشف الأقسام التالية (3-5) كيف يمكن وصف كل مستوى من مستويات إعادة التمثيل المرسومة مسبقًا في مصطلحات النمذجة الحسابية هذه.
3. المستوى 1 – إعادة تمثيل الميزات ككائنات وصور مختلفة
يشير المستوى الأول إلى القدرة على إعادة تمثيل الميزات ككائنات وصور مختلفة. تتم معالجة مهام الأرقام الغامضة في القسم 3.1. يتم استكشاف مهام النمط ومعنى الخط معًا في القسم 3.2. يقدم القسم 3.3 ملخصًا قصيرًا لسمات إعادة التمثيل التي تمت ملاحظتها تحليليًا على هذا المستوى.
3.1. أرقام غامضة
يمكن اعتبار الإدخال الموضوعي في شكل البطة والأرنب بمثابة مجموعة من الميزات المرئية. الإخراج عبارة عن صورتين (أو تفسيرات للصور). المعرفة الموجودة مسبقًا هي معرفة الكائن الممثل في الصورة، أو في بعض الأحيان الإلمام بمثل هذا النوع من تمثيل هذا الكائن3 .
من أجل تفسير هذه الميزات على أنها جزء من كائن وتمثله، يجب تحديد مجموعة فرعية من هذه الميزات وتجميعها ومطابقتها لكائن أو صورة معروفة. يمكن تجميع بعض هذه المجموعات من الميزات مسبقًا في مجموعات ميزات يمكن تعيينها إلى أجزاء كائن مختلفة، كما هو موضح في الشكل 5 (أسفل). في هذه الحالة، تتم مطابقة مجموعات السمات المختلفة مع أجزاء من جسم الحيوان والتي يُنظر إليها على أنها مخرجات. ومع ذلك، يمكن تفسير مجموعات الميزات المختلفة على أنها أجزاء مختلفة من الجسم، كما هو موضح في الشكل 5 (الأوسط). ومن ثم، فإن رؤية البطة أو الأرنب يمكن أن تعتمد على الأجزاء التي سيتم تفسير مجموعات المعالم هذه عليها.
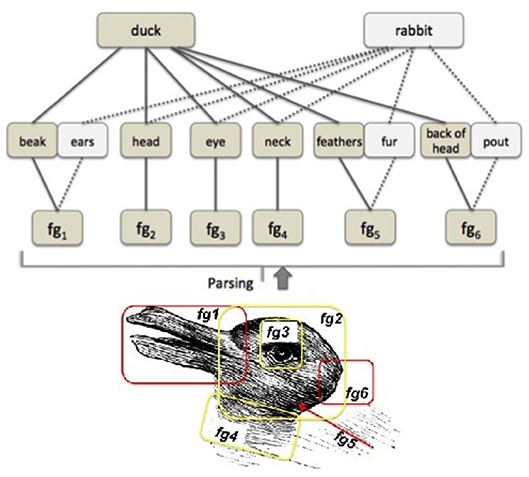الشكل 5 . شخصية البطة والأرنب غامضة. (أسفل) انقسم إلى مجموعات مميزة. (أعلى) مع مجموعات الميزات ( fg x , x ∈{1, 2, …, 6}) تم تحليلها كأجزاء كائن (حيوان).
في الحالة المبينة في الشكل 5 ، يتم تفسير مجموعة السمات fg 1 على أنها منقار أو أذنين ، وfg 5 على أنها نسيج ريش أو فرو ، و fg 6 على أنها الجزء الخلفي من الرأس أو العبوسقد يحدث فرقًا كبيرًا في رؤية إحدى الصورتين أو الأخرى. من غير الواضح الترتيب الذي تتم به العملية: ربما (1) تقوم الأنظمة المعرفية بإلقاء السمات بشكل مباشر من حيث تفسير أو آخر (نظرة من الأعلى إلى الأسفل)، أو (2) المجموعات المختلفة من الميزات تثير الجسم الأجزاء، والتي تؤدي بعد ذلك إلى تفسير الصورة (عرض من الأسفل إلى الأعلى) أو تلك (3) إحدى الميزات، التي يركز عليها النظام، تؤدي إلى ظهور الصورة الأكبر، والتي بدورها تؤدي إلى تفسير أجزاء الجسم (أ) منظر مختلط)4 .
ومع ذلك، فمن الواضح أن (صور) البط والأرانب لا بد أنها تمت مواجهتها سابقًا. القدرة على التبديلبين هذه التمثيلات هي القدرة على (أ) التبديل بين التعيين المحتمل للميزات (الموضوعية) لمجموعات ميزات و/أو كائنات مختلفة أو (ب) التبديل بين التفسيرات المختلفة لمجموعات الميزات هذه ككائنات. في حالة وهم البطة والأرنب، قد يتأثر التبديل جيدًا بـ (ب) – القدرة على إعادة تصنيف إحدى المجموعات الأولية لمجموعات السمات باعتبارها جزءًا مختلفًا من جسم الحيوان. ومع ذلك، في حالة الأشكال الغامضة المختلفة، حيث لا يمكن تخصيص مجموعات المعالم بدقة شديدة لتفسير واحد أو آخر، قد تحتاج مجموعات الميزات نفسها إلى إعادة تجميع مختلفة لتتمكن من رسم خريطة لأجزاء مختلفة من الجسم (أو ضمن رسم الخرائط) . وبالتالي (ج) قد تلعب القدرة على التبديل بين الكائنات المختلفة كتفسيرات محتملة للميزات، وبالتالي ترتيبها في مجموعات الميزات. تمثل المفاتيح الثلاثة جوانب مختلفة لعملية إعادة التمثيل.
قبل الانتقال إلى مهمة النمط ومعاني الخطوط، تجدر الإشارة إلى أنه ليست كل السمات الغامضة تتعلق بإعادة تمثيل السمات البصرية كمجموعات مختلفة أو تفسير هذه المجموعات كفئات مختلفة. على سبيل المثال، في وهم عازفة الساكسفون ( الشكل 6أ)، العلاقات بين مجموعات الميزات ليست واحدة لواحد بين الصورتين. يبدو أن التبديل بين التمثيلين في مثل هذه الحالات يتم بمعزل عن مستوى تفسير مجموعات الميزات كأجزاء مختلفة، على مستوى اختيار الميزات التي سيتم تجميعها للبدء بها. وبالتالي، فإن تجميع الميزات المطلوبة لتصنيف الساكسفون يمنع بالفعل تجميع أنف الفتاة وذقنها وظلالها، في حين أن تجميع فم الفتاة يمنع جزءًا من معطف عازف الساكسفون. يظهر هذا أيضًا في مشاكل الاستبصار، حيث قد تؤدي رؤية كائن واحد بقدرة معينة إلى إعاقة الحلول التي تتضمن نفس الكائن بقدرات مختلفة.
الشكل 6 . أوهام مختلفة. (أ) عازفة الساكسفون. (ب) ثلاثة تفسيرات غامضة الشكل.
علاوة على ذلك، فإن مثل هذه العلاقات في بعض الأحيان لا تكون بين مجموعات السمات البصرية، بل بين تفسيرات العلاقات المكانية. على سبيل المثال، يظهر الشكل 6ب صورة بثلاثة تفسيرات محتملة. يعتمد التبديل بين اثنين من هذه المكعبات – سواء تم النظر إلى المكعبات الثلاثة على أنها تشكل كومة على الأرض أو معلقة من السقف – على ما إذا تم تفسير أسطح معينة على أنها فوق أو تحت أسطح أخرى، وما إذا تم التركيز عليها كجزء من مكعب معين أو آخر. إذا تم إدراك الأشكال دون إسقاط علاقات العمق عليها، فسيتم إدراك صورة مختلفة (ثنائية الأبعاد).
3.2. معاني النمط والخط
في مهام النمط ومعاني الخط، لا يزال الإدخال عبارة عن مجموعة من الميزات. يتكون الإخراج من كائنات مختلفة ومجموعات من الكائنات والمشاهد المحتملة (على سبيل المثال، أشخاص ينتظرون في خط تمثيل الشكل 2أ ) كتفسير. المعرفة الموجودة مسبقًا هي المعرفة بالأشياء المذكورة ومجموعات الأشياء والسياقات والعلاقات والمشاهد، والتي يتم بعد ذلك التأثير على التفسير.
يمكن ملاحظة تداخل إعادة التمثيل مرة أخرى: يمكن إسقاط كائنات مختلفة على المجموعة الأولية من الميزات. تقدم مهمة النمط ومعاني الخط شكلاً مختلفًا من تمثيل وإعادة تمثيل مستوى الميزات، بمعنى أنه يمكن إجراء تفسيرات متعددة، ويمكن مطابقة مجموعة الميزات مع مجموعة أوسع بكثير من الصور المرئية. في الواقع، إذا كانت الأرقام الغامضة تستوعب بشكل عام ثلاثة تفسيرات محتملة كحد أقصى، فيمكن تفسير معاني النمط والخط على أنها مجموعة مقيدة فقط بأوجه التشابه المميزة مع الحافز المقدم في البداية. وبالتالي فإن منبهات النمط والخط من مثل هذه المهام تكون أكثر غموضًا بكثير من الأشكال الغامضة (على الرغم من اسم المهمة)، إذا كان مقياس الغموض هو عدد التعيينات التي يمكن إجراؤها من المحفز إلى تمثيلات الأشياء أو المشاهد المعروفة.
تعد محفزات الشكل أيضًا أكثر تجريدًا من تلك المقدمة في مهمة الأشكال الغامضة، ويجب إضافة العديد من الميزات لإنشاء تمثيل كامل. يمكن اعتبار الأشكال الغامضة بمثابة محفزات “مجردة” أيضًا بالطبع، بمعنى أنها ليست تصويرًا كاملاً ثنائي الأبعاد للكائن (مثل الصورة الكاملة)، ولكنها رسومات أو رسومات تخطيطية. ومع ذلك، فإن مجموعات الميزات الموجودة في الأشكال الغامضة تحتوي على معلومات أكثر بكثير حول الشكل الذي يتم تمثيله، وبالتالي تشكل تمثيلاً أكثر اكتمالاً.
تعتمد الأرقام الغامضة على تحديد نمط معروف بالفعل، والذي كان موجودًا مسبقًا في ذاكرة النظام (أو تمت تجربته بشكل مشابه)، حيث تتمثل المهمة الرئيسية في التمييز بين الميزات التي يجب أخذها في الاعتبار وفي أي منها دور. تعتمد مهمة الأنماط ومعاني الخطوط بشكل أكبر على الذاكرة، حيث يمكن استنباط العديد من الأنماط المتشابهة المعروفة، وبمعنى ما، كلما زاد عدد هذه الأنماط التي اكتسبها النظام، زاد أدائه المحتمل في مثل هذا الاختبار، إذا كان إعادة تمثيلية القدرات موجودة (وبالتالي إذا كان بإمكان المشارك التبديل بسهولة من تمثيل واحد للميزة الأولية التي تم تعيينها إلى آخر). ويمكن قول الشيء نفسه عن اختبار معاني الخط ( والاش وكوجان، 1965).)، مع الاختلاف الوحيد وهو أنه بينما يجب تفسير اختبار معنى الخط دون مقاطعة الخط، فإن التعيين في اختبار معاني النمط قد يكون من أجزاء متعددة من الميزة المعينة لكائنات متعددة. قد يكون لهذه الكائنات سياق مشترك: على سبيل المثال، تفسير الدوائر الأربع في الشكل 2أ على أنها رؤوس زهور يقيد تفسير المستطيل غير المكتمل باعتباره وعاء زهور، في حين أن تفسير نفس الدوائر مثل مقاعد البار أو الكراسي يقيد سياقيًا تفسير المستطيل غير المكتمل مستطيل كشريط أو جدول.
على الرغم من أن الكائنات والمشاهد التي تتم مطابقة الأنماط لها يجب أن تكون موجودة بالفعل في قاعدة المعرفة للنظام المعرفي لحل المهمة، فإن نظرة على بعض الإجابات التي قدمها الأشخاص عند محاولة هذه المهمة تظهر بالضبط مدى تنوعها وتعددها. الأوجه قدرة الإنسان على إعادة التمثيل.
تظهر التفسيرات المقدمة للشكل 2أ ، من بين أمور أخرى، القدرة على النظر إلى المشاهد وتخيلها من وجهات نظر مختلفة: على سبيل المثال، يتم عرض المقاعد المرتفعة أمام الطاولة من الأعلى؛ يمكن رؤية رؤوس الزهور القادمة من إناء زهور مستطيل من الأمام وربما من نفس الارتفاع، ويمكن رؤية لعبة مهد نيوتن مقلوبة (وتحتوي على أربع كرات فقط)، وما إلى ذلك.
مثال آخر مثير للاهتمام لإعادة التمثيل في مهمة معاني النمط موضح في الجدول 1 . هنا، تم تصوير النمط المعطى كحافز، إلى جانب مجموعة فرعية من 11 إجابة قدمها مشارك بشري، بصريًا. نظرًا لأن الإجابات قد تم تقديمها شفهيًا، فقد لا يكون هذا التصوير المرئي هو بالضبط ما كان يدور في ذهن المشارك، لكننا حاولنا ذلك من أجل عرض التشابه البصري للإجابات مع محفز النمط. وكما يتبين من الجدول 1 ، فإن الإجابات متنوعة تمامًا والتشابه مرن للغاية. إن الأوضاع التمثيلية للأشياء التي تتم مقارنة التشابه بها هي أيضًا متنوعة ومرنة تمامًا.
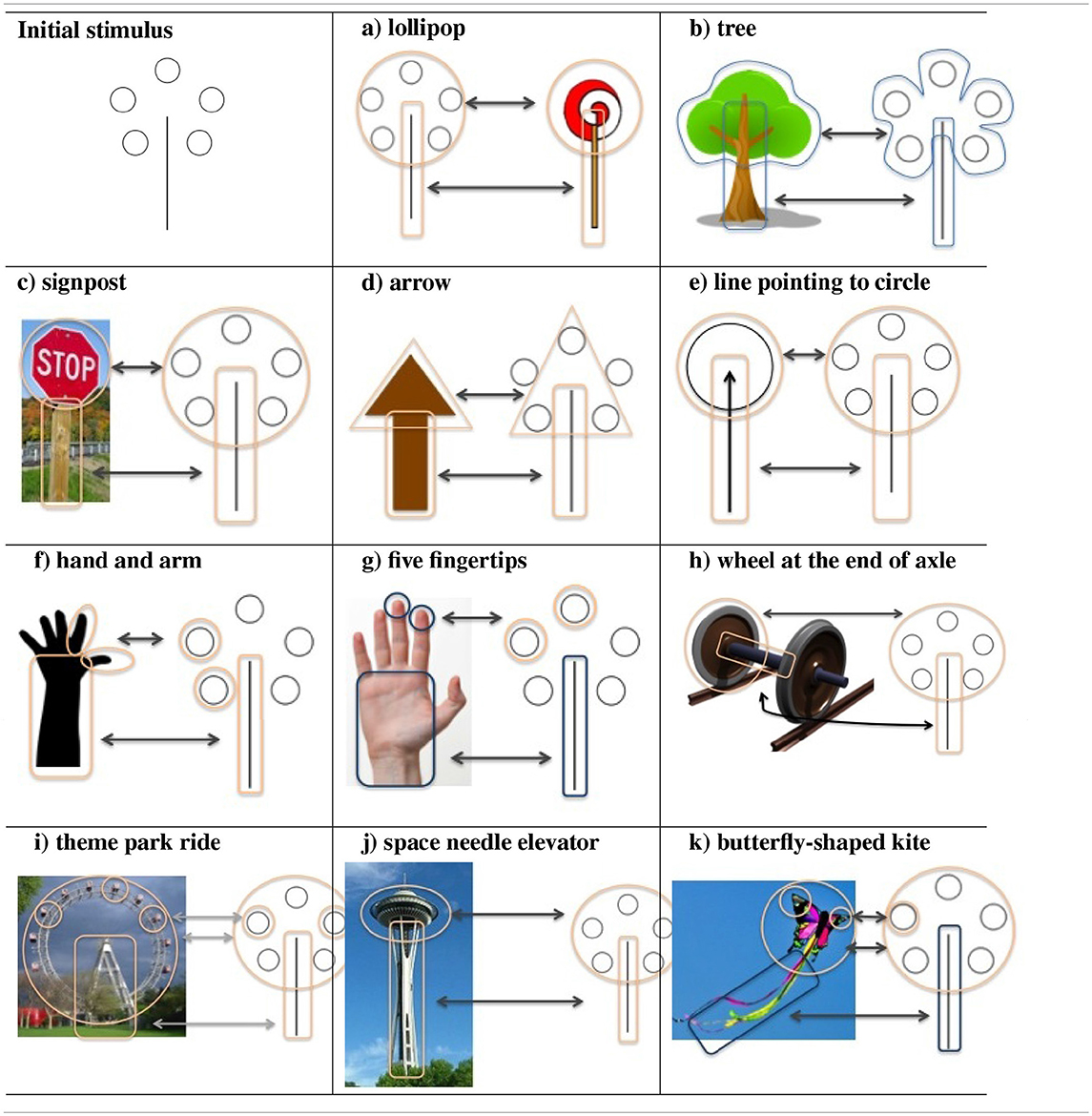الجدول 1 . سلسلة من الإجابات من قبل أحد المشاركين على نمط يعني التحفيز، وتم التأكيد على تصويرها البصري وأنواع التشابه مع التحفيز.
إن إجراءات تفسير الأجزاء المختلفة من المحفزات كمجموعة تلعب دورًا منذ البداية. نرى أيضًا إجراءات الإكمال الجشطالية، وبالتالي يتم تفسير الدوائر الخمس للمحفز الأولي على أنها تمثل دائرة في مجموعة متنوعة من الإجابات، كما في (أ)، (ج)، (هـ)، وما إلى ذلك. ونلاحظ إجراءات مثل الإمالة للأشياء المختلفة – مثل الدائرة في (ح)، العجلة والمحور ، أو الجذع في (ك)، إجابة الطائرة الورقية على شكل فراشة . نلاحظ تعديلات الشكل الكنتوري: على سبيل المثال، يجب ضغط الدائرة في المحفز الأولي إلى شكل بيضاوي لتتناسب مع (ي)، مصعد إبرة الفضاء. توجد أنواع أخرى من إكمال النمط: على سبيل المثال، يبدو أن محيط الدوائر الخمس هو الذي يحدد الإجابات (ب) و(ك). يتم اختيار ثلاث دوائر فقط للمجموعة المطلوبة في سهم الإجابة (د) ، ويتم إكمال النمط على شكل مثلث – تشكل الدوائر الثلاث رؤوسه. قد يلعب الرقم دورًا في الإجابات (و) اليد والذراع و (ز) خمسة أطراف أصابع . الإجابة (1) تحتوي رحلة المنتزه الترفيهي على خريطة للدوائر الأولية ودائرة الإكمال التخيلي، بينما من المحتمل (و)، ولكن بشكل أكثر وضوحًا (ز) ترسم خريطة للدوائر الأولية أيضًا.
تتحدث هذه الأمثلة عن عملية تحليل وإعادة تحليل الميزات الأولية، أثناء استخدامها للبحث من خلال مجموعة متنوعة من الكائنات المعروفة، في ميول وأوضاع متعددة. إلى جانب كونها إجابات، يمكن أيضًا تفسيرها على أنها مقارنات مرئية (خيالية) للأشياء المعروفة مع السمات الموجودة للمحفز، أثناء البحث عن التطابقات المحتملة.
أيضًا، يمكن أن توجد أنواع مختلفة من التشابهات، اعتمادًا على الخصائص المرئية المعنية – على سبيل المثال، يمكن تعيين مجموعة من ميزات محيط الشكل المأخوذة في البداية من الفطر إلى شكل آيس كريم، ولكن مجموعة مختلفة (على سبيل المثال، التصدعات تحت غطاء الفطر) يمكن أن يؤدي إلى إمكانية إعادة تمثيل الفطر كمظلة. وبالتالي فإن أجزاء من النمط البصري قد تؤدي إلى تفسيرات محتملة معينة، في حين أن ميزات أخرى قد تؤدي إلى تفسيرات أخرى5 .
3.3. ملخص – المستوى 1
يشير المستوى الأول إلى تفسير مجموعات الميزات المجمعة أو غير المجمعة كصور أو أشياء أو مشاهد معروفة محتملة. المدخلات في هذه الحالة هي الميزات. الإخراج عبارة عن صور، كما هو الحال في مهمة الأشكال الغامضة، والأشياء أو المشاهد، كما هو الحال في مهمة معاني الأنماط ومعاني الخطوط. يجب أن تكون هذه الكائنات معروفة مسبقًا، على الرغم من أن مقدار المعرفة المحدد الذي تتطلبه كل مهمة يمكن أن يكون مختلفًا.
إن عملية إعادة التمثيل هي، في هذه الحالة، عملية تعيين مجموعة من ميزات الإدخال لأنواع مختلفة من الكائنات والمشاهد المعروفة، والتبديل بين هذه التعيينات المختلفة. يتم تفسير هذا الإخراج على أنه تم تمثيله، بشكل غير مكتمل، في المدخلات: كرسومات تخطيطية (أشكال غامضة)، أو كإشارات إلى كائن أو مجموعة من الكائنات/المشهد البصري (في مهام معاني الخطوط ومهام معاني الأنماط).
4. المستوى 2 — إعادة تمثيل الكائنات والخصائص ككائنات مختلفة
يشير المستوى الثاني إلى القدرة على استخدام الأشياء الموجودة كما لو كانت كائنات أخرى ( يمكن استخدام الصحيفة كمظلة أو يمكن استخدام الكوب كجرس ) والتوصل إلى استخدامات إبداعية للأشياء الموجودة (مثل علبة حذاء صوفية يستخدم لمسح أسطح المطبخ). بعض هذه الأشكال من الاستدلال الإبداعي غير كاملة: قد تكون بعض الخصائص و/أو بعض أجزاء الكائن مفقودة من الكائن الأولي، حتى يتم تحويله بشكل صحيح أو إعادة تمثيله ككائن مختلف. مثال على الخصائص المفقودة: مجلة مصنوعة من ورق لامع، ويفضل أن تكون كبيرة الحجم، يمكن أن تعمل بشكل أفضل كمظلة من الصحيفة؛ بعض خصائص الصحيفة (كونها مصنوعة من الورق) لا تكفي لإنجاز المهمة كمظلة. أما بالنسبة للأجزاء المفقودة، فالكوب ليس جرسًا بعد، فهو لا يزال يحتاج إلى أجزاء أخرى، ربما ملعقة لضربه بها أو أي شكل آخر من أشكال المصفق6 .
المدخلات إلى المستوى الثاني هي الكائنات وخصائصها. والنتيجة هي (أ) أشياء أخرى و/أو (ب) إمكانيات جديدة للأشياء الموجودة في الحالة المحددة لاختبار الاستخدامات البديلة.
الناتج هو كائنات أخرى (الحالة أ)، عندما تتم إعادة التمثيل بشكل علني، بالإشارة إلى الأشياء: يمكنني استخدام حذاء إذا لم يكن لدي مطرقة، لدق المسمار . فالحذاء والمطرقة معروفان بالفعل، في حين أن الاستدلال الإبداعي قد يكون معروفًا أو يتم إجراؤه على الفور . إذا كانت إعادة التمثيل موجودة بالفعل على هذا المستوى، فإن التأكيد ” يمكن استخدام الكوب كجرس” حيث يمكن أخذه حيث يمكنني إعادة تمثيل الشكل والخصائص المادية للكوب كجسم الجرس . في حالة أكثر عمومية، يمكن اعتبار تأكيدات النموذج يمكنني استخدام الكائن A لاستبدال الكائن B، في سياق المهمة X على أنهايمكنني إعادة تمثيل (مجموعة فرعية من) ميزات وخصائص الكائن B، أو الميزات والخصائص المطلوبة للمهمة X، ككائن A.
يمكن أن يكون الناتج قدرة على تحمل التكاليف (الحالة ب)، كما هو الحال في اختبار الاستخدامات البديلة، عندما تكون الإجابة المقدمة من أحد المشاركين هي أنه يمكن استخدام الطوب لضرب مسمار، ودفعه عبر الحائط. يمكن إجراء إشارة سرية إلى الأشياء المعروفة التي قام الشخص بهذه المهمة بها (مثل المطرقة أو الحجر) في هذه العملية. يجب أن يكون الكائن الأولي والكائن المرجعي الخفي وإمكانياته معروفة جميعًا من أجل الاستدلال الإبداعي الذي سيتم تحقيقه. يمكن أخذ الإجابات التي تقول إن الطوب يمكن استخدامه لضرب مسمار، حيث يمكنني إعادة تمثيل (مجموعة فرعية من) ميزات وخصائص المطرقة، التي لديها القدرة على وضع مسمار في الحائط، كطوب . بشكل أكثر عمومية، يمكن اعتبار الإجابات من النوع الذي يمكنني استخدام الكائن A للقدرة على تحمله X على أنهايمكنني إعادة تمثيل (مجموعة فرعية من) ميزات وخصائص الكائن B، أو الميزات والخصائص المرتبطة بالقدرة على تحمل التكاليف X، ككائن A.
مجموعة صغيرة من الإجابات على سؤال اختبار الاستخدامات البديلة ” ما الذي يمكنك استخدام الكوب فيه؟” هو مبين في الجدول 2 . يُظهر العمود الثالث كائنات إعادة التمثيل العلنية والسرية المحتملة. كما هو مذكور أعلاه، قد يتم ذلك مع أو بدون مراجع الكائنات السرية؛ إذا تم ذلك بدونها، فيمكن أن تعتمد هذه الاستدلالات على مجموعات موجودة من الخصائص (من كائنات سابقة) والتي تحدث مع أداء مهمة معينة.
الجدول 2 . يستخدم البديل اختبار المثال، ويظهر الإجابات المستنبطة وإعادة تمثيل الكائن المحتمل للكأس .
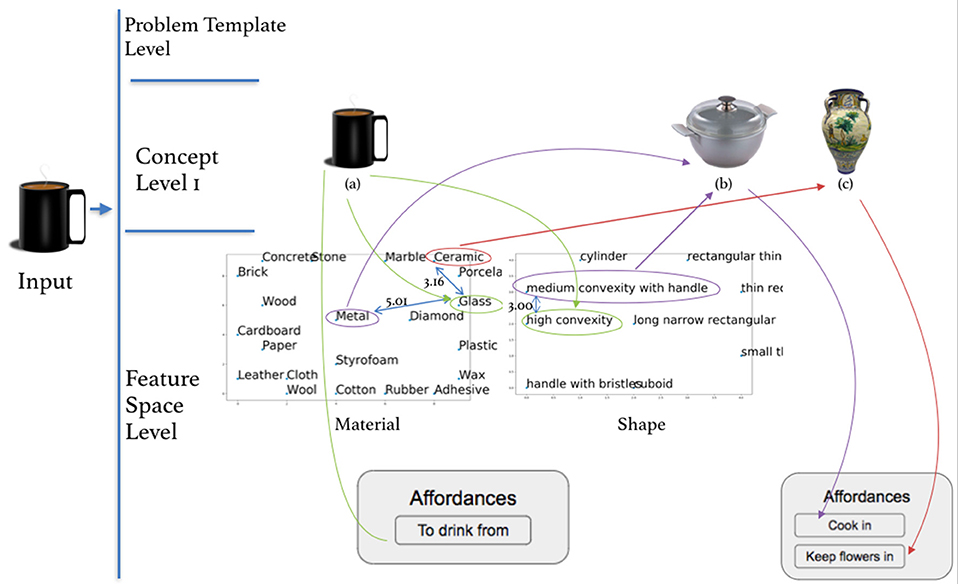
مثال على تنفيذ هذه المبادئ هو نظام OROC ( Olteţeanu and Falomir, 2016 )، الذي يستخدم المعرفة بمادة الكائن وشكله وخصائصه الأخرى لإجراء عمليات استبدال واستدلالات للكائن بأسلوب AUT، مما يوضح أن نفس النواة يمكن تطبيق العملية على كلا النوعين من المهام. يوضح الشكل 7أ الحالة التي تحتاج فيها شركة OROC إلى العثور على كائن بديل للكوب . قامت OROC سابقًا بتشفير الكوب بمجموعة من المواد والشكل والحجم والقدرة على تحمل التكاليف وغيرها من الخصائص. ثم يستخدم نوع تنظيم المعرفة الخاص به للبحث عن الكائنات الأخرى التي قام بتشفيرها في خصائص الكائن المطلوب – وبالتالي العثور على كائنات المهمة واقتراحها مثل Bowl ،مزهرية ودلو ، لهما نفس المادة والشكل.
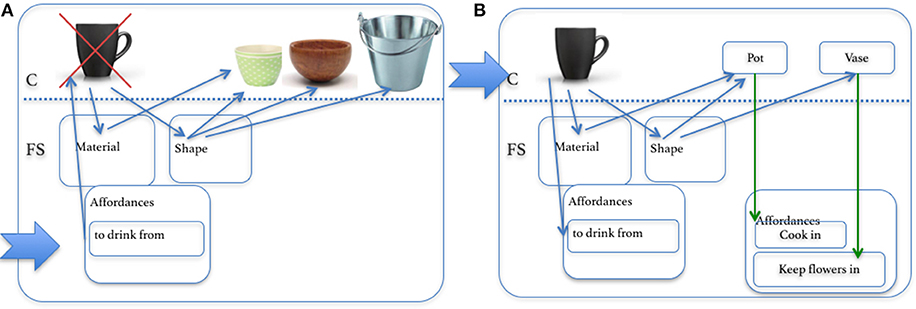الشكل 7 . استخدام إعادة تمثيل الخصائص لاستبدال الكائن (أ) وإجابات الاستخدام البديل (ب) في OROC. تتبع العملية اتجاه الأسهم.
وبالمثل، مع امتداد بسيط لهذه العملية، تقترح OROC إمكانيات لكائن معين، وبالتالي تكون قادرة على الإجابة على أسئلة AUT. ويبين الشكل 7B هذه العملية. الكائنات التي يشترك معها الكائن الأولي في خصائص (مشابهة) مثل الشكل والمادة لها إمكانيات يتم نقلها إلى الكائن الأولي. يمكن تفسير ذلك على أنه عملية إعادة تمثيل لكائن (أو مجموعة فرعية من خصائصه) من خلال المعرفة والخصائص المتعلقة بكائن آخر. وبالتالي يتم إعادة تمثيل الكوب على هيئة وعاء أو وعاء أو مزهرية ، ومن ثم يتم ربط إمكانيات هذه الأشياء بالكوبكاستدلالات إبداعية للاستخدامات الممكنة. يستخدم OROC كائنات مشابهة لتكوين الكائنات الإبداعية.
وبالتالي، في حالة هذا المستوى، فإن ما يتم إعادة تمثيله هو كائن، أو مجموعات من أجزاء الكائن وميزاته وخصائصه، ككائنات مختلفة. من الممكن أن تكون هذه الخصائص قد تم حفظها و/أو تنظيمها بالفعل في ذاكرة الحل أو العامل الإبداعي، أو أن ميزات الكائن المحدد يتم إعادة تمثيلها من أجل إنتاج استخدامات جديدة مخصصة .
5. المستوى 3 – إعادة تمثيل الأشياء والمشكلات
ومن أجل عرض إعادة التمثيل على مستوى مشاكل الاستبصار، سيتم تحليل حالة مشكلة الاستبصار هذه، وهي مشكلة تنطوي على أشياء عملية. إن استخدام مشكلات الاستبصار العملية للكائنات يجعل من الممكن دراسة حالة جديرة بالسبب الواضح وهو أن إعادة التمثيل (التمثلات) في مثل هذه المشكلة أسهل بكثير في التحدث عنها بعبارات محددة (حول الأشياء والإجراءات والخطط والإمكانات) مقارنة بمسائل الاستبصار المجردة. (والتي قد تنطوي على إعادة تمثيل مجردة).
في حالة المسائل العملية المتعلقة برؤية الأشياء، يكون الإدخال عبارة عن مشهد مرئي – وهو عبارة عن مجموعة من الكائنات أو مجموعات الكائنات، في علاقات مختلفة مع بعضها البعض7 . الناتج عبارة عن خطة عمل لكيفية حل مشكلة معينة – وهي عبارة عن مجموعة من الإجراءات باستخدام الكائنات، ووضع الكائنات في علاقات مختلفة في العملية8 . وهذا يتطلب المعرفة الموجودة حول الأشياء، وخصائص الكائن، والأجزاء والعلاقات، والإجراءات مع الأشياء وعواقب هذه الإجراءات. نحن نطلق على المعرفة المتعلقة بمجموعات الأشياء، والأفعال التي تتضمنها وعلاقاتها، وعواقب هذه الأفعال قوالب المشكلات ( Olteţeanu, 2014 ). ربما تم تعلم قوالب المشكلات هذه أثناء التفاعل مع الأشياء، أو من خلال التواصل. إن عواقب قوالب مشكلة معروفة معينة قد تكون أو لا تكون مفيدة في التوصل إلى حل لمشكلة حالية معينة.
في عملية حل مشكلة الاستبصار، تتضمن إعادة التمثيل رؤية المشكلة بطريقة مختلفة، أي إعادة صياغة المشكلة في قوالب مشكلة مختلفة، أو قوالب كائنات، أو تمثيلات أخرى موجودة مسبقًا. ستصبح هذه المصطلحات أكثر وضوحًا عندما نلقي نظرة على مسألة السلسلتين. يتم عرض هذه المشكلة كما هو موضح في الشكل 8 . يقال للمشارك: يتم وضع شخص في غرفة بها خيطين معلقين من السقف. عليهم ربط السلسلتين معًا. فكيف يمكنهم فعل ذلك، وهم يعلمون أنه من المستحيل الوصول إلى وتر واحد أثناء الإمساك بالآخر؟
الشكل 8 . مشكلة السلسلتين.
أثناء محاولة حل هذه المشكلة، يتوصل المشاركون البشريون إلى أجزاء محتملة مختلفة من الحل (كما هو موضح في تجربة التفكير بصوت عالٍ) أو بتركيبات تشير إلى عملية إعادة تمثيل كائنات المشكلة من خلال قوالب مختلفة للمشكلة والإجراء، أو قوالب الكائنات. على سبيل المثال، يحاول بعض الأشخاص بناء حلول تتضمن:
• الصعود على الكرسي . يتطلب ذلك تجميع عناصر الكائن الموجودة في مشكلة صغيرة أو قالب إجراء مثل ذلك الموضح في الشكل 9أ ، والذي يؤدي نتيجة لذلك إلى أن يكون الشخص في المشكلة في منصب أعلى؛ يعتقد بعض المشاركين أن كونهم أعلى سيسمح لهم بالوصول إلى مسافة أبعد عن طريق الإمساك بأحد الخيوط في نقطة مختلفة؛
• طرق الحبال إلى السقف (يتم توفير ذلك عن طريق الصعود على الكرسي أولاً). يتضمن ذلك إعادة تمثيل عناصر المشكلات مثل المسمار والكماشة من خلال المعرفة الموجودة أو قطع التمثيل، مثل تلك الموضحة في الشكل 9ب ؛ في هذه العملية يتم أيضًا إعادة تمثيل الكماشة كمطرقة؛
• ورق لف ، كما هو موضح في الشكل 9ج – يكون هذا مفيدًا عندما يتم إعادة تمثيل الورق نفسه كامتداد سلسلة أو موصل سلسلة، كما في الشكل 9هـ ؛
• دحرجة قميص الشخص الموجود في الغرفة إلى قطعة من الحبل، كما هو موضح في الشكل 9د . يسمح هذا مرة أخرى بإعادة تمثيل واستخدام كائن القميص كشكل من أشكال كائن الحبل؛
• ربط الخيوط أو العناصر التي يمكن إعادة تمثيلها كخيط ( ورقة ، تيشيرت ) ، كما في الشكل 9هـ ، أحياناً بغرض تطويلها أو السلسلتين الأوليين.
• استخدام الكماشة للإمساك بأحد الخيوط المعلقة من السقف، وبالتالي من المحتمل استخدام الكماشة وتمثيل الأسلاك مثل تلك الموجودة في الشكل 9F لإعادة تمثيل الكماشات الموجودة والأشياء الشبيهة بالأسلاك (مثل الأوتار)؛ في سياق هذه المشكلة، فإن استخدام الكماشة للإمساك بالخيط يؤدي أيضًا إلى إطالة متناول اليد؛
• أو الحل الفعلي المعترف به لهذه المشكلة، وهو بناء بندول مثل ذلك الموجود في الشكل 9ز . يتم ذلك عن طريق استخدام خيط وجسم ثقيل في الغرفة (مثل الكماشة ) ، وربط الجسم الثقيل بأحد الخيوط، واستخدام قدرته الجديدة كبندول لتحريكه، وجعله يتحرك نحوك بينما أنت يتمسكون بالسلسلة الأولى. وهذا يتطلب إعادة صياغة أو إعادة تمثيل السلسلة والكماشة أو كائنات السلسلة والجرة و/أو خصائصها من خلال قالب البندول. وبالتالي، يتم استخدام قالب كائن لإعادة تمثيل جزء من كائنات المشكلة، مما يؤدي إلى نوع جديد من القدرة على تحمل التكاليف، وحل ممكن.
الشكل 9 . تصوير مرئي لتمثيلات مختلفة تستخدم لتنظيم أو إعادة تمثيل الكائنات المشكلة عند حل مشكلة خيطين – من (أ) طرق مسمار في الحائط إلى (ز) البندول.
قد تتضمن بعض أجزاء حل المشكلات تجميعًا بسيطًا للعناصر الموجودة (مثل الشكل 9أ ) في تمثيل موجود، وتكون واضحة ومباشرة. قد يتضمن البعض الآخر أشكالًا أكثر تعقيدًا من إعادة التمثيل، حيث يتم استبدال كائنات مختلفة بأشياء أخرى – مثل تثبيت الحبل في السقف بمطرقة غير موجودة (الشكل 9ب) – والتي يجب إعادة تمثيلها من كائن آخر (الكماشة ) أو مجموعة الميزات الخاصة به.
علاوة على ذلك، فإن استخدام قوالب مختلفة يسمح بنشر الآخرين، كما هو موضح في الأمثلة السابقة: التسلق على الكرسي جزء ضروري من طرق الحبال إلى السقف؛ يعد لف الورق أو القماش أمرًا ضروريًا في نشر قالب آخر يتضمن إطالة الحبال وربطها، أو أي كائنات يتم إعادة تمثيلها الآن على أنها حبال، وما إلى ذلك. قد تكون بعض مجموعات الكائنات والتمثيلات ذات المستوى الأعلى لمجموعات من الكائنات كوحدة وظيفية واحدة وبالتالي يؤدي إلى تجميع الكائنات الأخرى في المشهد بطريقة معينة، بنفس الطريقة التي قد يؤدي بها تفسير مجموعة من الميزات المرئية كجزء من مجموعة معينة إلى تفسيرات محتملة موجودة بالفعل للصورة بأكملها أو مرتبطة بها9 .
إن استخدام تمثيلات معينة يمنع أو على الأقل يعيق استخدام تمثيلات أخرى. على سبيل المثال، إذا تم إعادة تمثيل الكماشة كمطرقة وجزء من خيط تثبيت في السقف باستخدام قالب مشكلة مسمار، فقد يواجه المحللون البشريون صعوبات في إعادة تمثيل (نفس الكماشة) كوزن، وجزء من قالب البندول . وهذا مشابه لما لاحظناه في حالة بعض الأشكال الغامضة – عندما يتم تمثيل مجموعة واحدة من السمات على أنها أنف، لا يمكن تمثيلها أو مجموعة فرعية متداخلة على أنها ساكسفون في نفس الوقت. وبالتالي، فإن إعادة التمثيل مطلوبة هنا أيضًا، ولكن على مستوى مختلف.
لاستكشاف ما إذا كان يمكن العثور على العلاقات بين هذه المهام تجريبيًا، وبالتالي يمكن دراسة إعادة التمثيل على مستويات متعددة، تم نشر دراسة تتضمن هذه المهام وتم الإبلاغ عنها في القسم التالي.
6. الدراسة
6.1. مشاركون
تم تجنيد عينة مكونة من 175 مشاركًا باستخدام Crowdflower، وتم استبعاد 37 منهم بسبب تقديم إجابات غير كاملة أو لا معنى لها. وأدى ذلك إلى حجم عينة إجمالي قدره 138 مشاركًا (63% إناث، 37% ذكور) تم استخدام إجاباتهم لمزيد من التحليل. تم تسجيل الأعمار باستخدام مقياس ترتيبي بفئات عمرية تبلغ 10 سنوات. كانت الفئات العمرية للمشاركين: أقل من 20 سنة ( ن = 8)، 20-30 سنة ( ن = 30)، 30-40 سنة ( ن = 49)، 40-50 سنة ( ن = 23)، 50-60 سنوات ( ن = 24)، 60-70 سنة ( ن = 3)، وأكثر من 70 سنة ( ن= 1). حصل معظم المشاركين على تعليم عالٍ حيث أكمل 58 (42٪) دورات جامعية و 16 (11.6٪) أكملوا دورات الدراسات العليا. التحق تسعة (6.5%) في دورات الدراسات العليا، و12 (8.7%) في الدورات الجامعية، وأنهى 31 (22.5%) شهادة الدراسة الثانوية، وأنهى 12 (8.7%) دراستهم الثانوية. باستخدام مقياس ليكرت المكون من 5 نقاط، تم جمع التقييمات الذاتية لكل من الإبداع ( المتوسط = 2.81، SD = 1.04) وحل المشكلات ( المتوسط = 2.88، SD = 0.96).
لم تكن موافقة لجنة الأخلاقيات ضرورية وفقًا لمؤسستنا والمبادئ التوجيهية الوطنية، لأنه لم تكن هناك مخاطر مرتبطة بالدراسة. تم منح موافقة مستنيرة عبر الإنترنت من قبل المشاركين لاستخدام البيانات مجهولة المصدر لأغراض البحث. تلقى المشاركون دفعة في Crowdflower لمشاركتهم.
6.2. طريقة
6.2.1. مهمة الأرقام الغامضة
لهذه المهمة، تم استخدام خمس صور مختلفة تظهر شخصيات غامضة. عُرضت على المشاركين الصورة لأول مرة وسُئلوا عما رأوه. وبعد ذلك، تم إبلاغهم بالشخصيتين المختلفتين اللتين يمكن رؤيتهما في الصورة. وسئلوا عما إذا كان بإمكانهم رؤية كلا الرقمين. تم بعد ذلك عرض كل صورة على المشاركين لمدة دقيقة واحدة، بينما طُلب منهم التبديل عقليًا بين الأشكال والضغط على زر كلما تمكنوا من رؤية الشكل الآخر. تم تسجيل كل من عدد الضغطات على المفاتيح والوقت المنقضي بين الضغطات.
6.2.2. اختبار معاني النمط
في اختبار معاني الأنماط، عُرض على المشاركين ستة أنماط مختلفة تتألف من كائنات هندسية مجردة بسيطة، واحدًا تلو الآخر. لقد طُلب منهم كتابة “أكبر عدد ممكن من الأشياء التي يمكنهم التوصل إليها حول ماهية الشيء.” تم تسجيل الوقت الذي استغرقه المشارك لكل نمط وإجاباته.
6.2.3. مهمة الاستخدامات البديلة
تم منح المشاركين شيئًا يستخدم يوميًا، ويجب عليهم توفير أكبر عدد ممكن من الاستخدامات البديلة له. تم تكرار هذا الإجراء لخمسة كائنات مختلفة. وكانت تلك الأشياء هي السجاد والصحف والأكواب وخيط تنظيف الأسنان وفرشاة الأسنان . مرة أخرى، تم تسجيل الإجابات ومقدار الوقت الذي استغرقه المشاركون لكل كائن.
6.2.4. مهام البصيرة
تم تقديم مشكلتين في الرؤية للمشاركين: مشكلة الشمعة ومشكلة وزن جاك وجيل. لقد تم توجيههم إلى أن هذه المسائل يمكن أن يكون لها عدة إجابات محتملة وأنهم يجب أن يفكروا في الحلول الممكنة ويكتبوها. وقد صيغت المشاكل على النحو التالي:
” يتم إعطاؤك شمعة وعلبة مسامير وكتاب أعواد ثقاب. من المفترض أن تقوم بتثبيت الشمعة المضاءة على الحائط بطريقة لا تسمح للشمع بالتنقيط بالأسفل. ماذا تفعل؟ “(مشكلة الشمعة).
” يتجادل جاك وجيل حول من يزن أكثر. ماذا يمكنهم أن يفعلوا لمعرفة ذلك على وجه اليقين؟ “(مشكلة وزن جاك وجيل).
كانت كل مشكلة مصحوبة بصورة، وكلاهما يمكن العثور عليهما في الملحق ، بالإضافة إلى محفزات الصور الخاصة بالمهام الأخرى. تم إعطاء المهام دائمًا بنفس الترتيب. ومع ذلك، تم عرض المحفزات في كل فئة بطريقة عشوائية.
6.3. نتائج
6.3.1. مهمة الأرقام الغامضة
يمكن رؤية نتائج مهمة الأرقام الغامضة في الجدول 3 ، الذي يوضح متوسط عدد المفاتيح في الدقيقة لكل رقم، بالإضافة إلى متوسط جميع التجارب. بالإضافة إلى ذلك، يتم عرض الانحرافات المعيارية. يشير متوسط الوقت حتى التبديل إلى مقدار الوقت المنقضي في المتوسط حتى يتم الإبلاغ عن التبديل بين التمثيلين. على سبيل المثال، بالنسبة للصورة 1، أنتج المشاركون في المتوسط 19.64 ضغطة مفتاح ( SD = 21.12)، وكانوا قادرين على التبديل بين التمثيلات كل 3 ثوانٍ تقريبًا.
الجدول 3 . نتائج مهمة الأرقام الغامضة.
بالإضافة إلى ذلك، تم رسم عدد الضغطات على المفاتيح مع مرور الوقت لجميع المشاركين باستخدام مضلعات التردد. تم ذلك بالنسبة للصور من 1 إلى 5 بشكل فردي ولجميع الصور مجتمعة. ويمكن رؤية هذه الرسوم البيانية في الجدول 4 .
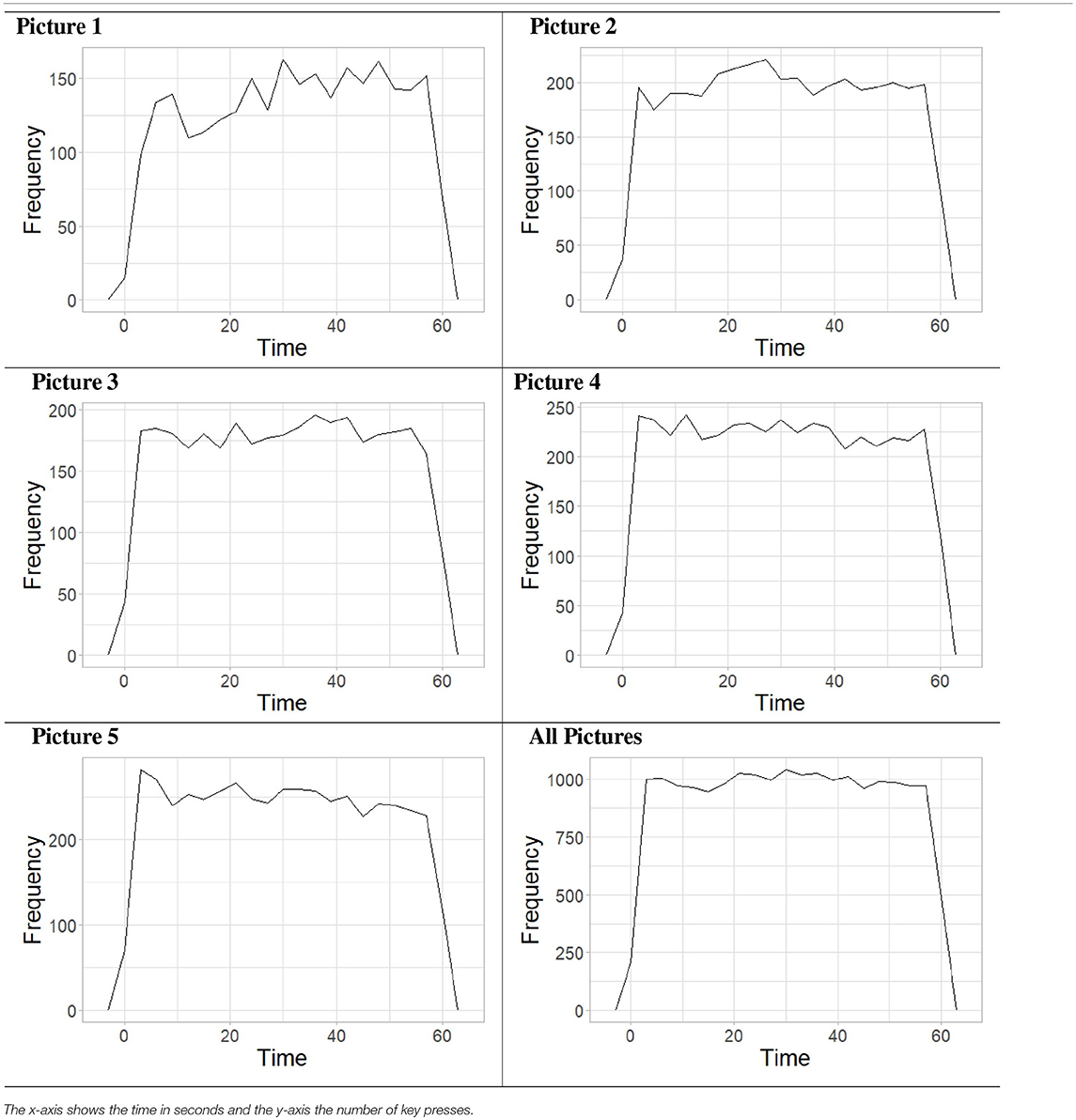الجدول 4 . تكرار الضغط على المفاتيح بمرور الوقت لكل صورة من الصور المستخدمة في مهمة الأشكال الغامضة، وكذلك لجميع الصور المجمعة، المعروضة في مضلع التردد.
6.3.2. اختبار معاني النمط
وتظهر نتائج اختبار معاني الأنماط في الجدول 5 . الطلاقة هي عدد الإجابات المقدمة؛ تقيس المرونة عدد المجالات الدلالية التي تغطيها هذه الإجابات، بناءً على التقييمات البشرية. بالإضافة إلى ذلك، تظهر أوقات الاستجابة لكل نمط (الوقت الذي يستغرقه المشارك لإعطاء جميع الإجابات)، وأوقات الاستجابة لكل معنى . لم يتم تسجيل أوقات الاستجابة لكل معنى بشكل مباشر، بل يتم حساب متوسطها من عدد الاستجابات المنتجة وإجمالي وقت الاستجابة لكل نمط.
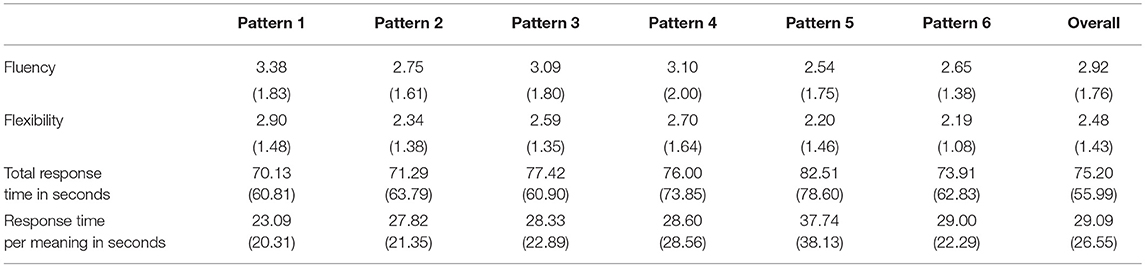الجدول 5 . نتائج اختبار معاني الأنماط: القيم المتوسطة والانحرافات المعيارية (بين قوسين) للطلاقة والمرونة وزمن الاستجابة الإجمالي وزمن الاستجابة لكل معنى.
6.3.3. مهمة الاستخدامات البديلة
ويمكن الاطلاع على النتائج في الجدول 6 . تشكل الطلاقة والمرونة نفس المقاييس كما في اختبار معاني النمط، فقط لعدد الاستخدامات البديلة المسماة لكل كائن معين . يمكن أيضًا العثور على أوقات الاستجابة لكل كائن ووقت الاستجابة لكل استخدام في الجدول.
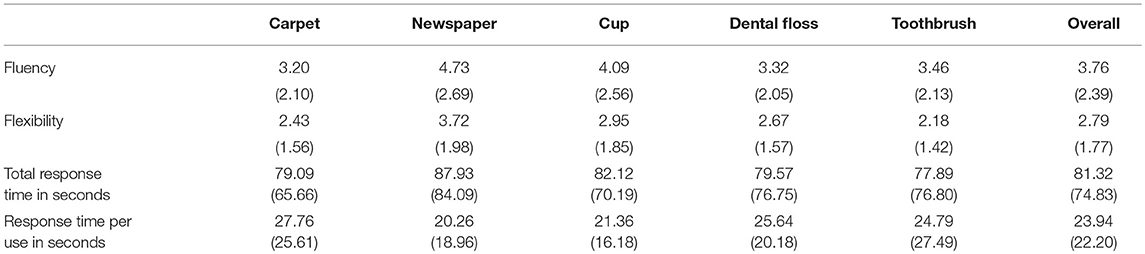الجدول 6 . نتائج مهمة الاستخدامات البديلة: القيم المتوسطة والانحرافات المعيارية (بين قوسين) للطلاقة والمرونة وزمن الاستجابة الإجمالي وزمن الاستجابة لكل استخدام.
6.3.4. مهام البصيرة
تم تقييم الإجابات من حيث صحتها. حصلت الإجابات التي تضمنت أجزاء من الحل الصحيح على درجة 0.5. بالنسبة لمسألة الشمعة، كان لدى 51 مشاركًا (37%) الإجابة الصحيحة، بينما أجاب 48 (35%) بشكل صحيح جزئيًا، ولم يعط 39 (28%) الإجابة الصحيحة على المشكلة. توصل أربعة مشاركين (3%) إلى الحل الصحيح لمشكلة وزن جاك وجيل، وأجاب واحد (1%) بشكل صحيح جزئيًا.
6.3.5. تحليل الموثوقية
لتحليل الموثوقية، تم حساب ألفا كرونباخ للطلاقة في اختبار معاني النمط (α = 0.91)، في مهمة الاستخدامات البديلة (α = 0.93) ولعدد الضغطات على المفاتيح في مهمة الأشكال الغامضة (α = 0.89). وبما أن جميع القيم وصلت إلى مستويات مرضية، فقد تم حساب القيم المتوسطة لكل مهمة واستخدامها كمؤشر للأداء.
6.3.6. مقارنة التدابير
إن مؤشرات الطلاقة المحسوبة في كل من اختبار معنى النمط ومهمة الاستخدامات البديلة، وكذلك الأداء في مهمة الأشكال الغامضة، كانت مرتبطة ببعضها البعض. تم العثور على علاقة إيجابية قوية (وفقًا لكوهين، 1992 ) بين الأداء في اختبار معاني النمط ومهمة الاستخدامات البديلة ( r = 0.77، p <0.001). كان لارتباطات قيم الطلاقة في اختبار معاني النمط ( r = 0.32، p <0.001) وفي مهمة الاستخدامات البديلة ( r = 0.37، p <0.001) مع مهمة الأشكال الغامضة حجم تأثير متوسط.
تم استكشاف العلاقة المحتملة بين الأداء في مشاكل الاستبصار والمهام الأخرى باستخدام اختبار كروسكال واليس حسب الرتب. نظرًا لأن عددًا قليلاً جدًا من المشاركين لديهم الإجابة الصحيحة على مشكلة الوزن جاك وجيل، فقد تم أخذ الإجابات على مشكلة الشمعة فقط في الاعتبار. توضح الأشكال 10 – 12 المخططات الصندوقية التي تستخدم الأداء في مشكلة الشمعة كمتغير تجميع. وتمت مقارنة أداء هذه المجموعات في مهمة الأشكال المبهمة واختبار معاني النمط ومهمة الاستخدامات البديلة باستخدام عدد الضغطات على المفاتيح والطلاقة كمؤشرات للأداء. كشف اختبار كروسكال واليس عن وجود اختلافات في الطلاقة في اختبار معاني النمط ( Cohen’s d = 0.476, p<0.05) ومهمة الاستخدامات البديلة ( Cohen’s d = 0.675، p <0.001)، ولكن ليس للأداء في مهمة الأشكال الغامضة ( p = 0.117، 1−β = 0.362). كشفت المقارنات الزوجية أنه بالنسبة لاختبار معاني الأنماط كان هناك اختلاف كبير بالنسبة للمقارنة الصحيحة – غير الصحيحة ( P <0.01). بالإضافة إلى ذلك، كانت هناك اختلافات كبيرة لمهمة الاستخدامات البديلة؛ هنا، اختلفت الطلاقة بشكل كبير بين المجموعتين صحيح – صحيح جزئيًا ( P <0.05)، وصحيح – غير صحيح ( P <0.001).
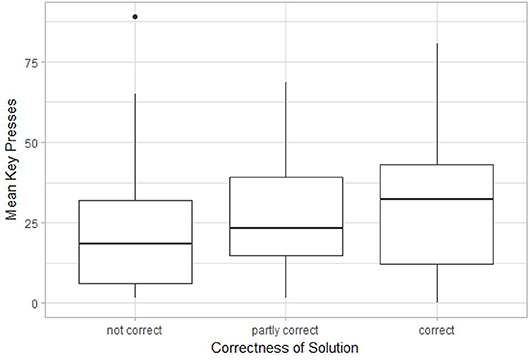الشكل 10 . Boxplot يقارن إجابات المشاركين (1) بمشكلة الشمعة (غير صحيحة أو صحيحة جزئيًا أو صحيحة)، مع (2) أدائهم في مهمة الأشكال الغامضة (يتم قياسها بعدد الضغطات على المفاتيح).
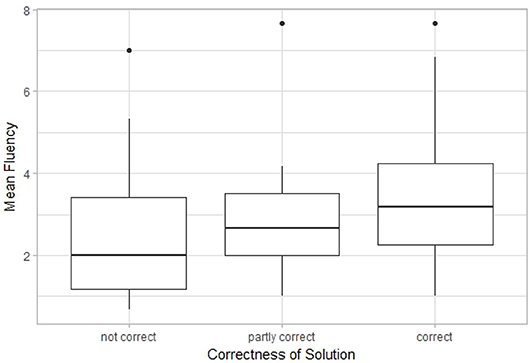الشكل 11 . Boxplot يقارن المشاركين الذين أعطوا إجابة لمشكلة الشمعة التي لم تكن صحيحة أو صحيحة جزئيًا أو صحيحة من خلال أدائهم في اختبار معاني النمط، مقاسًا بالطلاقة .
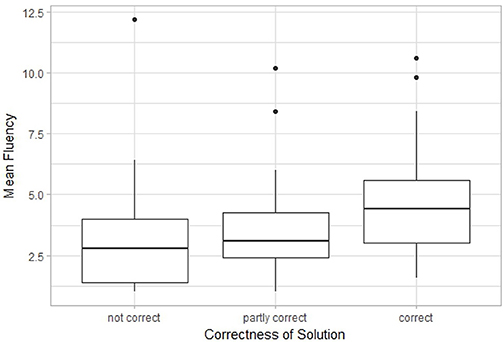الشكل 12 . Boxplot يقارن بين المشاركين الذين أعطوا إجابة لمشكلة الشمعة التي لم تكن صحيحة، أو صحيحة جزئيًا أو صحيحة من خلال أدائهم في مهمة الاستخدامات البديلة، والتي تم قياسها من خلال الطلاقة .
7. نموذج موحد لمستويات مختلفة من إعادة التمثيل
في هذا القسم، يتم عرض جميع مستويات إعادة التمثيل الثلاثة في سياق نموذج موحد.
مستوى مساحة الميزة : على مستوى مساحة الميزة، يتم تمثيل حافز الإدخال I رسميًا كمجموعة من الميزات:
حيث n = العدد الإجمالي للميزات الفردية المتصورة fg i = الميزة الأولى لتحفيز الإدخال. تتضمن إعادة التمثيل هنا مطابقة مجموعة فرعية من ميزات الإدخال مع الأنماط المرئية المعروفة؛ يتضمن هذا النوع من إعادة التمثيل تجميع الميزات ضمن أنماط معروفة مختلفة، والبحث عنها ومقارنتها بالأنماط والكائنات في قاعدة المعارف ثم تفسيرها كأحد هذه الأنماط أو الكائنات المعروفة.
أ) اختبار الأرقام الغامضة
وفي سياق الأرقام الغامضة، تتم إعادة التمثيل على النحو التالي. بالنظر إلى مشكلة الأرنب والبط في الشكل 5 ، عندما يتم تجميع مجموعة السمات fg 1 – fg 6 معًا وتتم مطابقة fg 1 و fg 5 و fg 6 مع المحفز البصري للمنقار والريش ومؤخرة الرأس ، على التوالي ، يكون الشكل هو ممثلة على شكل بطة . على النقيض من ذلك، عندما تتوافق الميزات fg 1 و fg 5 و fg 6 مع المحفز البصري لـالأذنين والفراء والعبوس ، يتم تمثيل الشكل على شكل أرنب . إعادة التمثيل في هذه الحالة هي عملية إعادة تجميع المجموعات الأولية من الميزات بطرق مختلفة ومطابقتها لنمط مختلف.
ب) اختبار النمط ومعنى الخط
في سياق اختبار معاني الأنماط ( الشكل 13 )، عندما يركز الوكيل على جميع الميزات fg 1 − fg 6 و fg 1 − fg 5 يتم تجميعها معًا في جشطالت الدائرة، يمكن تمثيل/تفسير النمط على أنه مصاصة ( الشكل 13أ ). عندما يختار الوكيل ويجمع المعالم fg 1 و fg 3 و fg 5 كرؤوس مثلث ( الشكل 13ب )، يمكن إعادة تمثيل مجموعة المعالم كسهم. وبالمثل، عندما تكون استدارة fg 3 , fgتم التأكيد على الشكل 4 ومطابقتها لنمط مرئي معروف لأطراف الأصابع، ويمكن إعادة تمثيل مجموعة الميزات fg 3 و fg 4 و fg 6 على أنها خمسة أطراف أصابع وكف ( الشكل 13ج ). تتم عمليات إعادة التمثيل المختلفة على النحو التالي:
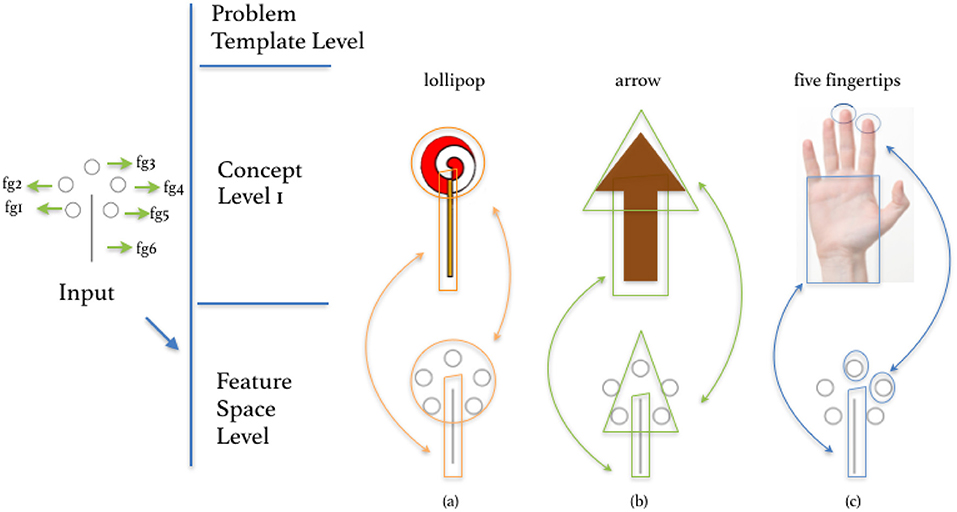الشكل 13 . يتم إعادة تمثيل الميزات ككائنات مختلفة في مهمة “معاني النمط”. (أ) المصاصة، (ب) السهم، و (ج) خمسة أطراف أصابع.
من المهم أن نذكر أنه حتى عندما يتم التركيز على نفس مجموعة الميزات، يمكن أن يكون هناك نتائج متعددة لإعادة التمثيل. على سبيل المثال، في نفس مجموعة الميزات يتم التركيز عليها في كل من (أ) و(ب)؛ ولكن في (أ) يتم إعادة تمثيل مجموعة الميزات كمصاصة بينما في (ب) كشجرة. إعادة التمثيل في هذه الحالة هي القدرة على إعادة تجميع الميزات وإعادة تعيينها إلى نمط أو كائن معروف مختلف.
مستوى المفهوم : مستوى الكائن لإعادة التمثيل يمكن أن يحدث على النحو التالي. في إطار عمل CreaCogs ( Olteţeanu وFalomir, 2016 ):
يشير fs_shape إلى مساحة ميزات الأشكال في قاعدة المعرفة (KB)،
يشير fs_material إلى المساحة المميزة للمادة الموجودة في قاعدة المعارف،
يشير fs_color إلى مساحة ميزات الألوان في قاعدة المعارف،
يشير fs_size إلى المساحة المميزة للارتفاع والعمق والعرض للكائنات في قاعدة المعارف،
يشير fs_affordance إلى المساحة المميزة للإجراءات/الحركات التي يمكن القيام بها باستخدام الكائن،
يشير fs_name إلى مساحة الميزات لأسماء الكائنات في قاعدة المعارف.
يتم وصف الكائن/المفهوم X في إطار عمل CreaCogs على أنه تنشيط لميزاته على النحو التالي:
وفقًا لمخطط إضفاء الطابع الرسمي هذا، يمكن وصف الكأس والمزهرية على النحو التالي:
تتم إعادة التمثيل على هذا المستوى عن طريق مقارنة الكائن الأصلي بالكائن الآخر من حيث خصائص الكائن مثل المادة والشكل والحجم وما إلى ذلك. وهذا موضح في الشكل 14 وقد تم تنفيذه حسابيًا في نظام يمكن أن يأتي مع استخدامات مختلفة للأشياء، من خلال إعادة صياغتها كأشياء لها خصائص متشابهة ( Olteţeanu and Falomir, 2016 ). في شكل أكثر عمومية، يمكن اعتبار تأكيدات النموذج يمكنني استخدام الكائن B لاستبدال الكائن A، في سياق المهمة X حيث يمكنني إعادة تمثيل (مجموعة فرعية من) ميزات وخصائص الكائن A (التي لها تم توصيله بالمهمة X) ككائن B .
الشكل 14 . يتم إعادة تمثيل الكائنات والخصائص ككائنات مختلفة. (أ) الكأس، (ب) القدر، (ج) المزهرية.
يثبت نظام OROC ( Olteţeanu and Falomir, 2016 ) أن شكل الوعاء ومادته ( “متوسط_التحدب_مع_المقبض”، “المعدن”) يشبهان شكل الكوب ( “التحدب_العالي”، “الزجاج”)، ويستخلص استنتاجات حول تنطبق إمكانيات الوعاء أيضًا على الكوب . وهذا شكل من أشكال إعادة تمثيل الوعاء على شكل كوب . وبالمثل، يمكن إعادة تمثيل ملامح الكوب على شكل مزهرية ، من خلال ملاحظة التشابه بين شكل ومادّة المزهرية وشكل الكوب . هذا الكأس الكائن (كما هو موضح في الشكل 14) وبذلك تخفف قيودها وترث إمكانياتها من الكائن المزهري :
مستوى قالب المشكلة : يتم تمثيل قالب المشكلة رسميًا كمجموعة من المفاهيم ( C i )، والعلاقات ( R i )، والإجراءات ( H i )، والأهداف ( G i )، والقيود ( Cx i ) . أين،
المفاهيم هي أشياء يومية لها خصائص مثل الشكل والمادة والحجم وما إلى ذلك.
العلاقات هي ارتباط بين مفهومين أو أكثر.
الإجراءات هي الإجراءات التي يتم تنفيذها على المفاهيم والتي قد تؤدي أو لا تؤدي إلى تغيير في العلاقة.
الأهداف هي مجموعة من المفاهيم والعلاقات.
تصف القيود حدود الموارد أو الإجراءات الخاصة بالمهمة.
بالنسبة لمشكلة السلسلتين، يمكن تصور المفاهيم والعلاقات والهدف والقيود على النحو التالي:
• ج 1 , ج 2 − السلسلة 1 , السلسلة 2
• ج 3 – شخص
• ج 4 − الكرسي
• ج 5 − كماشة
• ج 6 − جرة المسامير _ _ _
• ج 7 − أوراق_الورق _ _ _ _
• ج 8 − المسامير
• R 1 , R 2 − معلق ( سلسلة 1 , السقف ) , معلق ( سلسلة 2 , السقف )
• R 3 , R 4 , R 5 − على الأرض ( الكرسي ) , على الأرض ( أوراق _ ورق ) , على الأرض ( جرة _ مسامير ) , على الأرض ( مسامير )
• R 6 − يحمل ( شخص، سلسلة 1 )
• جي سول −{ التعادل ( السلسلة 1 , السلسلة 2 )}
• Cx 1 −if R x = يحمل ( شخص، سلسلة 1 )، إذن¬ Ry = الوصول ( شخص، سلسلة 2 )
مشكلة C = { C 1 , C 2 , C 3 , C 4 , C 5 , C 6 , C 7 , C 8 }
مشكلة R = { R 1 , R 2 , R 3 , R 4 , R 5 , R 6 }
مشكلة ح = {}
مشكلة G = { G sol }
مشكلة Cx = { Cx 1 }
أنا = { مشكلة C ، مشكلة R ، مشكلة H ، مشكلة G ، مشكلة Cx }
إعادة التمثيل هنا هي للكائنات ومجموعات الكائنات وقوالب المشكلات ككائنات مختلفة وقوالب مشكلة. ويبين الشكل 15 عمليات إعادة التمثيل على هذا المستوى في سياق مشكلة السلسلتين. المشكلة هي ربط السلسلتين معًا. كان قالب المشكلة الأصلي هو الشخص الذي يحاول الإمساك بالسلسلة الثانية أثناء الإمساك بالسلسلة الأولى. لكن القيد يمنع هذا الإجراء على وجه التحديد، لذلك يجب تشغيل قوالب المشكلات الأخرى وتطبيقها لإيجاد حل.
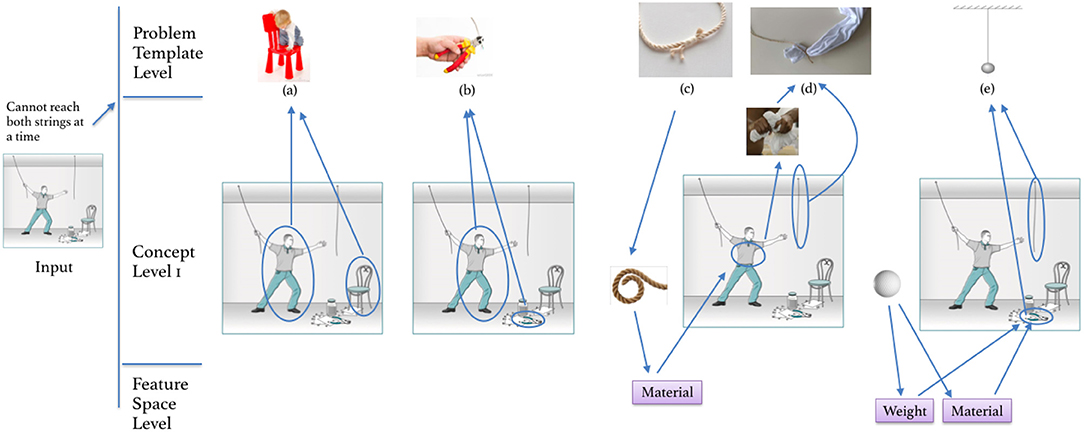الشكل 15 . الكائنات ومشكلة إعادة التمثيل في مشكلة السلسلتين. (أ) التسلق على قالب الكرسي، (ب) مد الذراع باستخدام الزردية، (ج) ربط حبلين، (د) ربط الحبل والقميص، (هـ) البندول.
في الشكل 15أ، يتم إعادة تمثيل المشكلة الأولية من خلال قالب حيث يحاول الشخص الإمساك بالسلسلة الثانية من ارتفاع مختلف، على افتراض أن هذا سيساعد في الوصول إلى أبعد من ذلك. وبالتالي يتم إعادة تمثيل الأشياء الموجودة في الغرفة ( الكرسي ، الوكيل ) كعناصر لهذه المشكلة. في الشكل 15ب، يتم تشغيل قالب محاولة الإمساك بالسلسلة الأخرى باستخدام الزردية. يمكن تحفيز ذلك إما من الأسفل إلى الأعلى — من الكائن إلى مستوى القالب (من خلال ملاحظة وجود الكماشات في غرفتهم والتفكير في وظائفها)، أو من الأعلى إلى الأسفل، من خلال التفكير في طرق لمد اليد (ستساعد الكماشات في الوصول إلى أبعد قليلا).
تُظهر الأشكال 15 د، هـ حالات أكثر إثارة للاهتمام من إعادة التمثيل، حيث أن إعادة التمثيل فيها تتم على مستوى قالب المشكلة والمفهوم. في الشكل 15د ، يُعاد تمثيل قميص الرجل على شكل حبل. ومن ثم، يتم إعادة تمثيل المشكلة الأصلية باستخدام قالب استطالة الخيط عن طريق عقد خيطين، حيث تم إرخاء القالب لربط القميص بالحبل. في الشكل 15هـ، يتم إعادة تمثيل الكماشات كوزن، ثم يتم إعادة تمثيلها مع الخيط كبندول. من المحتمل أن يتم تشغيل هذا الأمر من خلال استخدام نموذج المشكلة الذي يحتوي على معلومات حول تأرجح البندول لجعل الحبل يتحرك نحوك ويتيح لك ذلك. في جميع الحالات، يتم إعادة تمثيل المشكلة الأصلية بمساعدة قوالب مشكلة مختلفة، وفي بعض الأحيان يتم إعادة تمثيل الكائنات أيضًا. ويتم إضفاء الطابع الرسمي على إعادة التمثيل على هذا المستوى على النحو التالي:
I → { C 1, C 2, C 3} → PT(الأصلي):{ C = { C 1 , C 2 , C 3 }, R = { يحمل ( C 3 , C 1 )}, G = { ربطة عنق ( ج 1 ، ج 2 )}}
I → { C 2 , C 3 } → PT(elongate_string):{ C = { C 2 , Tshirt }، H = { Attach ( C 2 , Tshirt }، G = { C new = { سلسلة _ أطول }}
I → { C 2 , C 5 } → PT(make_pendulum):{ C = { C 2 , C 5 }, R = { مرفق { C 2 , C 5 }, H = { تأرجح ( C 2 )}, G = { ج جديد = { البندول }}
8. المناقشة
8.1. مناقشة النتائج
كان الهدف من هذه الدراسة هو التحقق مما إذا كانت هناك قدرة على إعادة التمثيل التي تكمن وراء الأداء في مهمة الأشكال الغامضة، واختبار معنى النمط، ويستخدم البديل الاختبار ومشكلات الاستبصار. والواقع أن العديد من النتائج التي تم الحصول عليها تؤدي في هذا الاتجاه. نتائج وايزمان وآخرون. (2011) و Doherty and Mair (2012) يمكن تأكيدهما من خلال إظهار الارتباطات بين مهمة الأشكال الغامضة ومهمة الاستخدامات البديلة، وكذلك بين مهمة الأشكال الغامضة واختبار معاني النمط، مع حجم مشارك أكبر بكثير. بالإضافة إلى ذلك، تم إظهار وجود علاقة ارتباط بين مهمة الاستخدامات البديلة واختبار معاني النمط، مع حجم تأثير أعلى بكثير.
تم استكشاف العلاقة المحتملة مع الأداء في مهام الرؤية باستخدام الأداء في مشكلة الشمعة كمتغير تجميع. وكان هذا بسبب عدة أسباب. أولاً، نظرًا لحقيقة أنه في هذه الدراسة تم تقديم مشكلتين فقط في الرؤية، لم يكن من الممكن استكشاف البيانات على مستوى الفاصل الزمني. أيضًا، تبين أن مشكلة وزن جاك وجيل كانت صعبة للغاية بالنسبة للمشاركين، لذلك لم يتمكن سوى عدد قليل جدًا من حلها. أدى هذا إلى حصر التحليل في المقارنة الجماعية، وتقسيم المشاركين على قدرتهم على تقديم حل صحيح أو صحيح جزئيًا على الأقل لمشكلة الشمعة. لم يكن هذا ممكنًا بالنسبة لمشكلة وزن جاك وجيل، حيث كانت المجموعات مختلفة جدًا في حجمها. ونظرًا لانتهاك افتراض الحالة الطبيعية، لم يكن من الممكن أيضًا إجراء تحليل التباين (ANOVA)، وبالتالي اقتصر التحليل على الاختبارات غير البارامترية. وكشفت هذه النتائج أنه في المتوسط، سيكون لدى الأشخاص ذوي معدلات الطلاقة الأعلى فرصة أكبر للإجابة على مسألة الشمعة بشكل صحيح، مما يشير إلى أن هذه المهام تشترك في سمات مشتركة. لا يبدو أن هذه الفكرة تنطبق على مهمة الأرقام الغامضة، على الرغم من أن هذه المقارنة تفتقر إلى القوة ويجب التحقيق فيها في الدراسات المستقبلية.
بشكل عام، تدعم نتائجنا فرضية القدرة الأساسية على إعادة التمثيل. إن الارتباطات بين مهمة الأشكال الغامضة، ومهمة معاني النمط، واختبار الاستخدامات البديلة توفر دليلا قويا على تلك الفكرة، كما أن نتائج مهمة الاستبصار، على الرغم من كونها استكشافية في طبيعتها، تظهر بعض الاتجاهات الواضحة. ولكن ما هو ملحوظ في النتائج الارتباطية التي تم الحصول عليها هو أنها لا تعكس بشكل مباشر هيكل المستوى المقترح، كما هو موضح في الشكل 4 .
إن ارتباط مهمة نمط المعاني مع مهمة الاستخدامات البديلة يظهر حجم تأثير أعلى من الارتباطين الآخرين. من نظريتنا، نتوقع أن نرى ارتباطًا وثيقًا بين مهمة الأشكال الغامضة ومهمة معاني النمط، حيث يتضمن كلاهما إعادة تمثيل الميزات، على عكس اختبار الاستخدامات البديلة، حيث يحتاج المشاركون إلى إعادة تمثيل الأشياء. الشيء الوحيد الذي يمكن أن يفسر هذا هو جانب الدافع. نظرًا لعدم وجود حد زمني معين لمهمة معاني الأنماط واختبار الاستخدامات البديلة، فقد يكون الدافع قد لعب دورًا مهمًا في المدة التي كان المشاركون يحاولون التوصل فيها إلى حلول جديدة. لم يكن هذا هو الحال بالنسبة لمهمة الأرقام الغامضة، حيث كان لدى المشاركين حد زمني قدره دقيقة واحدة تنتهي بعدها المهمة، لذلك ربما لم يكن هذا الدافع بنفس الأهمية.
قد يكون لحقيقة أنه في إحدى المهام تم تقديم التمثيلات المحتملة، بينما كان على المشاركين الآخرين تقديم تمثيلاتهم الخاصة، قد يكون لها أيضًا تأثير على تحفيز وأداء المشاركين. قد يكون للطلاقة اللفظية أيضًا تأثير على النتائج، حيث أن الأشخاص الذين لديهم طلاقة لفظية أعلى عمومًا قد يكونون أفضل في التوصل إلى المزيد من الإجابات في مهمة معاني الأنماط ومهمة الاستخدامات البديلة. في الدراسات المستقبلية، ينبغي دراسة تأثير هذه الإرباكات المحتملة والسيطرة عليها إذا لزم الأمر.
8.2. مناقشة عامة
وهكذا تم وصف ثلاثة مستويات من إعادة التمثيل، في سياق أربع مهام تجريبية. يمكن استخدام هذه المهام لاستكشاف العلاقة بين المستويات المختلفة ومقارنة النماذج الحسابية ومخرجات الأنظمة المعرفية الاصطناعية بالمخرجات البشرية. وبالتالي يمكن استخدام نوع مماثل من العمليات الحسابية لحل جميع هذه الأنواع من المهام، مع وجود اختلافات من حيث نوع المعرفة وكمية المعرفة المستخدمة.
على مستوى النظام الحسابي، يتطلب ذلك اتباع نهج متكامل للنمذجة متعدد المستويات: إطار موحد يتم من خلاله نمذجة جميع المستويات الثلاثة، والذي يتم فيه فقط إدخال المدخلات والمخرجات والوصول إلى كمية المعرفة المحفوظة التي يتم جلبها إلى العملية، لكن العملية تظل كما هي أو يتم تنفيذها بشكل مشابه. ويظهر ذلك في الشكل 16أ . وبدقة تفصيلية، في سياق المستويات التي تم تحليلها سابقًا، يبدو أن إعادة التمثيل هي عملية تجميع ميزات المدخلات المختلفة في مخرجات معروفة مختلفة محتملة، والتي تكون معروفة بالفعل (أو في هياكل مشابهة لتلك المخرجات) من أجل الحصول على وظائف مختلفةالتمثيل، أو الوصول إلى إمكانيات مختلفة مرتبطة بكائنات أخرى، أو الوصول إلى إجراءات محتملة مختلفة مرتبطة بقوالب مشكلة أخرى أو خطط عمل، أو تحويل التمثيل الأولي تمامًا، وإنشاء كائن جديد، أو قالب مشكلة، وما إلى ذلك .
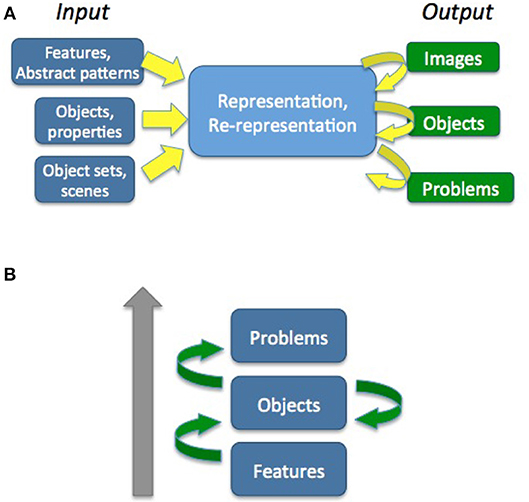الشكل 16 . إعادة التمثيل. (أ) نفس العملية، مع أنواع مختلفة من المدخلات والمخرجات؛ يتغير الإخراج كدالة للعملية. (ب) إعادة التمثيل (الأسهم الخضراء) التي تعمل عند مستويات مختلفة من التعقيد التمثيلي وفيما بينها.
تحدد مخرجات المستويات المختلفة التي تم وصفها هنا تفسير أو أنواع التمثيلات التي يتم إسقاطها على المدخلات بواسطة النظام المعرفي، أو الخصائص الثانوية التي قد تتبع من هذا التمثيل (مثل الإمكانيات الجديدة، والحلول الجديدة). في بعض الأحيان يكون ناتج التمثيل الجديد واضحا، وفي أحيان أخرى لا يمكن ملاحظة ذلك إلا بسبب خصائصه الثانوية.
كما هو مبين في الشكل 16Bيفترض هذا النهج أن إعادة التمثيل، التي تظهرها الأسهم الخضراء، تعمل بين مستويات متعددة من التعقيد التمثيلي. وبالتالي، يجب أن تكون الأطر أو البنى المعرفية التكاملية قادرة على نمذجة العملية وشرحها وعرضها على جميع هذه المستويات. إحدى الصعوبات المتأصلة في النمذجة على جميع هذه المستويات ستكون بالطبع إحدى الصعوبات التمثيلية. ولا ينبغي إهمال الآثار المتتالية المحتملة لإعادة التمثيل بين مستويات متعددة. على سبيل المثال، قد يؤدي التركيز على مجموعة فرعية مختلفة من الميزات إلى جعل القائم بالحل يرى كائنًا ما على أنه كائن محتمل مختلف، مما قد يؤهله للحصول على الإمكانيات والتجميع في مجموعة مختلفة من الكائنات التي قد تؤدي معًا إلى إعادة تمثيل المشكلة. قبل حساب مثل هذه التأثيرات المتتالية،
إن النظرة المتشابهة حسابيًا للعمليات المختلفة ستساعد في تبسيط نمذجة وتنفيذ كل من هذه العمليات والمهام في الأنظمة المعرفية الحسابية. وهذا سيسمح بمزيد من الدراسة لهذه المهام. إذا كانت العملية هي نفسها أو متشابهة بالفعل على المستويات الثلاثة المعبر عنها هنا، فإن هذا النهج التركيبي الموحد يجب أن يساعد في فهم إعادة التمثيل بطريقة أكثر وضوحًا من خلال الاستكشاف المقارن والتجريب لمستويات محددة، مع افتراض وجود اختلافات أولية في تعقيد التمثيل (و في معالجة تمثيلات مختلفة النوع و/أو التعقيد). لقد تم تناول الارتباط أو التشابه أو العمليات الأخرى التي قد تجعل إعادة التمثيل ممكنة في مكان آخر ( Olteţeanu, 2014 ; Olteţeanu and Falomir, 2015 ,2016 ).
وتشير النتائج الحالية لدراستنا إلى وجود علاقة بين المهام المقترحة. ومع ذلك، لم يتم الحصول حتى الآن على أي حجة تجريبية لصالح التسلسل الهرمي لإعادة تمثيل المستويات، ويشير أحد المراجعين بحق إلى أن كل هذه الأنواع من التمثيلات يمكن أن تتعايش بالتوازي. في العمل المستقبلي قد نكون قادرين على استخدام نموذج حسابي للتمييز بين هاتين الفرضيتين. ومع ذلك، فإننا نعتقد أن المستويات الثلاثة هي أدوات مفيدة للتفكير في أنواع المعلومات التي تتم معالجتها ووضع نماذج لها: الميزات والمفاهيم والأشياء وقوالب المشكلات (مجموعات من الكائنات والعلاقات والإجراءات).
في ورقتهم، أولينجر وآخرون. (2008) فحص كيفية تأثير المجموعة العقلية على عملية التغيير التمثيلي. تُعرف المجموعة العقلية بأنها الميل إلى حل مشكلات معينة بطريقة ثابتة بناءً على حلول سابقة لمشاكل مماثلة. في CreaCogs، العنصر المقابل للمجموعة العقلية هو التثبيت داخل قالب المشكلة الذي يتم تشغيله لحل المشكلة. قوالب المشكلات عبارة عن مجموعات منظمة من الإجراءات وطرق حل المشكلات المحفوظة في قاعدة المعرفة (أو ذاكرة الحل). وهي تعتمد على المعرفة السابقة بالأشياء وعلاقاتها وخصائصها وأفعالها وكيف حققت الأهداف السابقة. تعتبر المجموعة العقلية إحدى نتاجات عملية الاختيار ( Anderson, 1982 ; Newell, 1994 ;لوفيت وأندرسون، 1996 ) في CreaCogs، لا تزال مشكلة الاختيار قائمة، على الرغم من أنها ليست المشكلة التي نركز عليها في هذه الورقة. وهذا يعني أن المجموعة العقلية يمكن أن تحدث بسبب اختيار أحد قوالب المشكلة بشكل تفضيلي على القوالب الأخرى، ويجد الوكيل الذي يقوم بحل المشكلة صعوبة في إعادة تمثيل المشكلة عبر قالب يوفر المزيد من فرص النجاح. تتمثل إحدى طرق حل هذه المشكلة في CreaCogs في المستقبل في وضع افتراضات أو جمع بيانات حول مدى معرفة القوالب المختلفة لمختلف المحللين، ثم تشفير ذلك حسابيًا، من خلال إضافة أوزان إلى القوالب المختلفة.
في ورقة أولينجر وآخرين، يتضمن التغيير التمثيلي احتمالين على الأقل – تحلل القطع وتخفيف القيود. يشبه تحلل القطع تحلل الكائنات في CreaCogs، حيث يمكن تقسيم الكائن الذي يُنظر إليه ككل إلى الأجزاء المكونة له (أو مكونات فرعية أخرى)، ويمكن تطبيق مكوناته على حل المشكلة، أو إعادة تجميعها في كائن آخر التكوينات (نفس الشيء ينطبق على قوالب المشكلة). إن التوازي مع استرخاء القيد في CreaCogs هو تخفيف التحيزات الطبيعية والمكتسبة ضد كسر الأشياء، وذلك باستخدام قوالب المشكلات بطريقة مألوفة بالفعل، وتجاوز الفطرة السليمة أو معايير الممارسة الشائعة أو القيم الجمالية. وهذا يساعد على تسهيل عملية إعادة التمثيل.
أولينجر وآخرون. التركيز على تأثير الاستراتيجيات المختلفة، مثل تحلل القطع وتخفيف القيود (أو النوع القياسي فقط) على قدرة المشاركين الإضافية على حل المشكلات التي تتطلب نفس النوع أو أنواعًا أخرى من التغيير التمثيلي. ومع ذلك، فهي لا تشكل نموذجًا ولا تصف عملية التغيير التمثيلي من حيث يمكن أن تستخدم في التنفيذ الحسابي. لا تقدم هذه الورقة بيانًا بشأن كيفية تأثير التغيير التمثيلي لنوع واحد على أنواع أخرى من التغيير التمثيلي. وبدلاً من ذلك، فهو يركز على إيجاد المهام المختلفة التي يمكن من خلالها استكشاف واختبار عملية التغيير التمثيلي. تهدف هذه الورقة أيضًا إلى أن تتضمن هذه المهام التجريبية أنواعًا مختلفة من المحفزات، بدرجات مختلفة من تعقيد المعلومات، وتمثل مستويات معرفة مختلفة للعامل المعرفي والهندسة المعمارية. تم طرح آلية إعادة تمثيل أولية يمكن صياغتها حسابيًا لجميع مستويات المعلومات (والمحفزات).
يعد غموض المحفزات المختلفة أيضًا قضية مثيرة للاهتمام. في بعض الحالات، قد يسمح الغموض بإعادة تمثيل أسهل وأكثر إبداعًا، وربما يمكن اقتراح مقاييس حسابية للغموض على جميع المستويات الثلاثة. تخميننا الأولي هو أن مثل هذا القدر من الغموض سيتطلب الأخذ في الاعتبار عدد التمثيلات التي يمكن تحليل مشهد معين وتمثيله، والذي من المحتمل أن يعتمد على النظام المعرفي الذي يقوم بإعادة التمثيل. سيكون من الصعب قياس ذلك في الأنظمة المعرفية الطبيعية، على الرغم من أنه ربما يمكن تمييز مجموعة من الاحتمالات القوية المهيمنة لإعادة التمثيل لمجموعة معينة من المحفزات، من خلال التحقيق التجريبي. ومع ذلك، فإن القياس الحسابي للغموض سيكون مثيرًا للاهتمام وأكثر جدوى لنشره في الأنظمة المعرفية الاصطناعية.
لقد طرحت هذه الورقة نهجا متعدد الطبقات لإعادة التمثيل. ويهدف هذا النهج إلى دمج الأداء بشكل هادف في أربع مهام مختلفة لدراسة إعادة التمثيل كعملية معرفية واحدة. إذا ثبت أن الاختلافات القائمة على المعرفة بين هذه المستويات المختلفة تؤثر على العملية نفسها بطرق مهمة، فلا يزال من الممكن دمج إعادة التمثيل كفئة واحدة من العمليات. سيدعم هذا التكامل الدراسة التجريبية والحسابية الموحدة لفئة من عمليات حل المشكلات الإبداعية.
9. الخاتمة والعمل المستقبلي
اقترحت هذه الورقة أن إعادة التمثيل، وهي عملية أساسية في حل المشكلات الإبداعية والإبداع البشري، يمكن ويجب تحليلها بطريقة أكثر تكاملاً. ولتحقيق ذلك، تم استكشاف ثلاثة مستويات لإعادة التمثيل. وتم استخدام المهام لتجسيد وتحليل الخصائص التي تتخذها عملية إعادة التمثيل في كل مستوى من هذه المستويات، من أجل توضيح العملية نفسها.
أكدت دراسة تجريبية عبر هذه المهام فرضيتنا القائلة بأنه يمكن إنشاء علاقات بين هذه المهام، وكررت دراستين سابقتين مع عدد كبير من المشاركين، وكشفت عن علاقة جديدة قوية وهامة بين اختبار معاني الأنماط واختبار الاستخدامات البديلة.
كان اقتراحنا هو أن تتم صياغة عملية إعادة التمثيل على المستويات الثلاثة: (1) إعادة تمثيل الميزات كأشياء أو صور مختلفة، (2) إعادة تمثيل الأشياء وخصائصها كأشياء مختلفة، و (3) إعادة تمثيل الأشياء وخصائصها كأشياء مختلفة. تمثيل الكائنات ومجموعات الكائنات والمشاهد والمشكلات كقوالب كائنات ومشكلات مختلفة. وقد تم طرح نموذج أولي موحد لعملية إعادة التمثيل وعرضه على كافة هذه المستويات.
كعمل مستقبلي سوف نهدف إلى:
• إضفاء الطابع الرسمي على كل مستوى مقترح لإعادة التمثيل ;
• محاولة نمذجة المستويات المختلفة حسابياً ضمن نفس الإطار المعرفي.
• استكشاف العوامل الأساسية للأداء التجريبي في هذه المهام.
بيان الأخلاق
أجريت هذه الدراسة بموافقة خطية مستنيرة من جميع المواد. لم تكن موافقة لجنة الأخلاقيات ضرورية، حيث لم تكن هناك مخاطر مرتبطة بالدراسة. أعطت جميع المواد موافقة خطية مستنيرة وفقًا لإعلان هلسنكي.
الكاتب الاشتراكات
قام A-MO بوضع تصور وتنظيم الأساس النظري للمقالة. كتب A-MO الأقسام من 1 إلى 5 والمناقشة في القسم 8، بالإضافة إلى الخاتمة. A-MO وMS خططت ونشرت الدراسة التجريبية. تم تحليل البيانات بواسطة MS. كتب MS القسم 6. بعد المراجعة، حدد A-MO بحثًا جديدًا ليتم إضافته للرد على المراجعين، والنموذج الموحد. كتبت AB قسمًا جديدًا 7 وتمت إضافته إلى المناقشة. قام مرض التصلب العصبي المتعدد بتحليل كروسكال واليس وإضافته إلى المناقشة. أشرف A-MO على العملية وقام بمراجعة النص الجديد وتحسينه.
بيان تضارب المصالح
يعلن المؤلفون أن البحث تم إجراؤه في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
شكر وتقدير
A-MO تعترف بامتنان بدعم مؤسسة الأبحاث الألمانية (Deutsche Forschungsgemeinschaft) لمشروع الأنظمة المعرفية الإبداعية (CreaCogs) عبر المنحة OL 518/1-1. الصور المستخدمة لإنشاء الجدول 1 والشكل 9 تحمل ترخيص Creative Commons وتم وضع علامة عليها لإعادة الاستخدام مع التعديل. يُعتقد أن الصور الموجودة في الأشكال 1 و 6أ موجودة في الملكية العامة. ونشكر مؤلفيها لوضعها على الإنترنت.
المواد التكميلية
يمكن العثور على المواد التكميلية لهذه المقالة عبر الإنترنت على: https://www.frontiersin.org/articles/10.3389/fpsyg.2019.00940/full#supplementary-material
الحواشي
1. ^ الفرق بين اختبار معاني الخط واختبار معاني النمط هو أن الخط عبارة عن حافز مستمر، وتفترض بعض الإعدادات أنه لا ينبغي للمشاركين تقسيمه إلى أجزاء عندما يقدمون التفسير.
2. ^ يمكن مناقشة هذا المستوى من إعادة التمثيل على نطاق أوسع في سياق المفاهيم وخصائصها، بدلا من الأشياء. لقد اخترنا مناقشة حول الكائنات لأنه في هذه الحالة يكون تحديد الميزات أسهل، دون الوقوع في السؤال عن كيفية تمثيل المفاهيم وخصائصها. يتمتع هذا النهج بميزة أنه يمكنه دعم المستوى التالي – مستوى مشكلات الاستبصار – إذا كانت المشكلات التي تمت معالجتها تقع في مجال الكائن العملي.
3. ^ يمكن اعتبار هذا بمثابة الإلمام بأسلوب تمثيلي رسومي معين. على سبيل المثال، إذا لم يسبق لأحد أن رأى أرنبًا ممثلًا كشخصية ثنائية الأبعاد، في شكل أيقوني ومن المنظور الذي يتم تمثيله منه عادةً، فقد يتم إعاقة التفسير الأولي لمثل هذا الشكل على أنه أرنب.
4. ^ قد تكون أوامر العملية الأخرى ممكنة أيضًا. ما سنركز عليه هنا ليس الترتيب، بل على التفاصيل الخشنة للعملية التي يتم من خلالها تمثيل مجموعات مختلفة من الميزات وإعادة تمثيلها، أو إدراكها وإعادة تشكيلها/رؤيتها كأشياء مختلفة.
5. ^ لا يوجد بالطبع أي حدود من شأنها أن تقيد إعادة التمثيل في المجال البصري. ومع ذلك، فإن التمسك بالمرئيات يسمح لنا بإظهار الأشكال التي نعنيها.
6. ^ لسان الجرس أو ضاربه.
7. ^ ملاحظة: من المفيد التأكيد على أن الكائنات هي في حد ذاتها مجموعات: مجموعات من أجزاء الكائن، ويمكن أيضًا اعتبارها مجموعات من الخصائص، أو حتى الميزات.
8. ^ لأن الأشياء في العلاقات المختلفة قد يكون لها إمكانيات مختلفة.
9. ^ كما هو الحال في المقطع الذي يتحدث عن هذه العملية مع الصور، ليس الغرض من هذه الورقة وضع افتراض حول ما إذا كانت هذه العملية من أعلى إلى أسفل، أو من أسفل إلى أعلى أو تفاعل بين الاثنين، ولكن لعرض إعادة التمثيل في عموماً والحاجة إلى أطر معرفية تتكامل فيها مستوياته المتعددة .
مراجع
أندرسون، جي آر (1982). اكتساب المهارات المعرفية. نفسي. القس 89، 369-406. دوى: 10.1037/0033-295X.89.4.369
دوهرتي، إم جي، وماير، إس. (2012). الإبداع والشخصيات الغامضة والتفضيل الأكاديمي. التصور 41، 1262-1266. دوى: 10.1068/p7350
داو، جي تي، وماير، ري (2004). تعليم الطلاب حل مشكلات البصيرة: دليل على خصوصية المجال في التدريب على الإبداع. خلق. الدقة. ج 16، 389-398. دوى: 10.1080/10400410409534550
إيبي، إم، كونفالونيري، آر، ماكلين، إي، كالياكاتسوس، إم، كامبوروبولوس، إي، وشورليمر، إم (2015). “الاختراع الحسابي للإيقاعات وتقدم الوتر عن طريق مزج الوتر المفاهيمي،” في المؤتمر الدولي الرابع والعشرون المشترك حول الذكاء الاصطناعي (بالو ألتو، كاليفورنيا: مطبعة AAAI / المؤتمرات الدولية المشتركة حول الذكاء الاصطناعي).
فالكنهاينر، ب.، فوربس، كيه دي، وجينتنر، د. (1989). محرك رسم الخرائط الهيكلية: الخوارزمية والأمثلة عارف. إنتل. 41، 1-63. دوى: 10.1016/0004-3702(89)90077-5
فوكونير، ج.، وتيرنر، م. (1998). شبكات التكامل المفاهيمي. كوجن. الخيال العلمي. 22، 133-187. دوى: 10.1207/s15516709cog2202_1
جينتنر، د. (1983). رسم الخرائط الهيكلية: إطار نظري للقياس. كوجن. الخيال العلمي. 7، 155-170. دوى: 10.1207/s15516709cog0702_3
جيلفورد، جيه، كريستنسن، بي، ميريفيلد، بي، وويلسون، آر (1978). الاستخدامات البديلة: دليل التعليمات والتفسير . أورانج، كاليفورنيا: شيريدان للخدمات النفسية.
هوليواك، ك.، وثاغارد، ب. (1996). القفزات العقلية: القياس في الفكر الإبداعي . كامبريدج، ماساتشوستس: مطبعة معهد ماساتشوستس للتكنولوجيا.
جيلك، دي جي، ليبير، سي، أورايلي، آر سي، وأندرسون، جيه آر (2008). سال: بنية معرفية تعددية بشكل واضح. جي إكسب. النظرية. عارف. إنتل. 20، 197-218. دوى: 10.1080/09528130802319128
كيراس، دي، وماير، دي (1997). نظرة عامة على البنية الملحمية للإدراك والأداء مع التطبيق على التفاعل بين الإنسان والحاسوب. همم. حساب. يتفاعل. 12، 391-438. دوى: 10.1207/s15327051hci1204_4
ليرد، جي إي، نيويل، أ.، وروزنبلوم، PS (1987). ترتفع: بنية للذكاء العام. عارف. إنتل. 33، 1-64. دوى: 10.1016/0004-3702(87)90050-6
لاكوف، ج.، وجونسون، م. (1999). الفلسفة في الجسد: العقل المتجسد وتحديه للفكر الغربي . نيويورك، نيويورك: الكتب الأساسية.
لوفيت، ماك (1998). “الاختيار”، في المكونات الذرية للفكر ، محرران جي آر أندرسون، وسي. ليبير (Mahwah، NJ: Erlbaum)، 255–296.
لوفيت، MC، وأندرسون، JR (1996). تاريخ النجاح والسياق الحالي في حل المشكلات: التأثيرات المشتركة على اختيار المشغل. كوجن. نفسي. 31، 168-217. دوى: 10.1006/cogp.1996.0016
ماير، NR (1931). العقل عند البشر. ثانيا. حل المشكلة وظهورها في الوعي. جي قارن. نفسي. 12:181. دوى: 10.1037/h0071361
أولسون، س. (1983). إعادة النظر في إعادة الهيكلة: I. ملخص ونقد نظرية الجشطالت في حل المشكلات. سكاند. جي سيكولوجي. 25، 65-78. دوى: 10.1111/j.1467-9450.1984.tb01001.x
أولسون، س. (1984). إعادة النظر في إعادة الهيكلة: II. نظرية معالجة المعلومات لإعادة الهيكلة والبصيرة. سكاند. جي سيكولوجي. 25، 117-129. دوى: 10.1111/j.1467-9450.1984.tb01005.x
أولينجر، م.، جونز، ج.، وكنوبليتش، ج. (2008). بحث تأثير الضبط العقلي على حل مشكلة الاستبصار. إكسب. نفسي. 55، 269-82. دوى: 10.1027/1618-3169.55.4.269
أولتيتينو، أ.-م. (2014). “فئتان عامتان في حل المشكلات الإبداعي؟ “حساب يعتمد على العمليات المعرفية التي تنطوي عليها العلاقة بين بنية المشكلة وبنية التمثيل،” في وقائع ورشة العمل حول الإبداع الحسابي واختراع المفهوم والذكاء العام ، المجلد 01-2014 من منشورات معهد العلوم المعرفية ، محرران T. بيسولد، K.-U. كونبيرجر، م. شورليمر، وأ. سمايل (أوسنابروك: معهد العلوم المعرفية).
أولتيتينو، أ.-م. (2016). “من الآلات البسيطة إلى Eureka في أربع خطوات ليست سهلة. نحو الذكاء البصري المكاني الإبداعي،” في القضايا الأساسية للذكاء الاصطناعي ، المجلد 376 من المكتبة التركيبية ، الطبعة V. Müller (Cham: Springer)، 159–180.
أولتيتانو، أ.-م، وفالومير، ز. (2015). comRAT-C: حل اختبار مركب عن بعد حسابي يعتمد على بيانات اللغة ومقارنتها بالأداء البشري. بات. التعرف على. بادئة رسالة. 67، 81-90. دوى: 10.1016/j.patrec.2015.05.015
أولتيتانو، أ.-م، وفالومير، ز. (2016). استبدال الكائنات وتكوينها في النظام المعرفي الإبداعي. نحو حل حسابي لاختبار الاستخدامات البديلة. كوجن. النظام. الدقة. 39، 15-32. دوى: 10.1016/j.cogsys.2015.12.011
Olteţeanu، A.-M.، شوتنر، M.، وSchuberth، S. (2018). إحياء اختبار الزملاء الوظيفيين عن بعد حسابيًا باستخدام الكلمات المعرفية الزميلة والمبادئ من حل حسابي. نول. النظام القائم . 168، 1-9. دوى: 10.1016/j.knosys.2018.12.023
Olteţeanu، A.-M.، شولثيس، H.، وداير، JB (2017). إنشاء مستودع حسابي لعناصر اختبار Remote Associates المركبة باللغة الإنجليزية الأمريكية باستخدام comRAT-G. بيهاف. الدقة. طرق الوسيلة. حساب . 50، 1971–80. دوى: 10.3758/s13428-017-0965-8
أورايلي، RC (1996). نموذج ليبرا للتفاعلات العصبية والتعلم في القشرة المخية الحديثة . أطروحة دكتوراه، جامعة كارنيجي ميلون، بيتسبرغ، بنسلفانيا.
صن، ر. (2007). أهمية البنى المعرفية: تحليل يعتمد على الوضوح. جي إكسب. النظرية. عارف. إنتل. 19، 159-193. دوى: 10.1080/09528130701191560
فيلي، T.، وهاو، Y. (2008). “تمثيل المعرفة السائلة لفهم وتوليد الاستعارات الإبداعية،” في وقائع المؤتمر الدولي الثاني والعشرين للغويات الحاسوبية ، المجلد. 1 (جمعية اللغويات الحاسوبية)، 945-952.
ياريت تشكرونا على المجهود فى نقل وكتابه البوست ولو بتعليق
